Interval List Intersections

Interval List Intersections: You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [start_i, end_i] and secondList[j] = [start_j, end_j]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

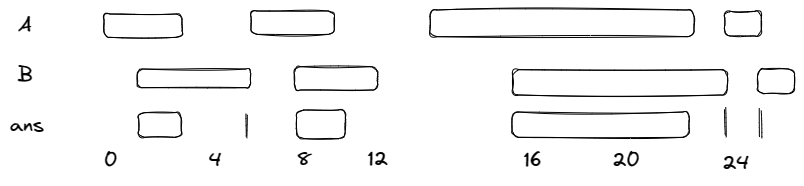
Input: firstList = [[0,2],[5,10],[13,23],[24,25]],
secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

Constraints:

0 <= firstList.length, secondList.length <= 1000
firstList.length + secondList.length >= 1
0 <= start_i < end_i <= 10^9
end_i < start_i+1
0 <= start_j < end_j <= 10^9
end_j < start_j+1

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
    if(firstList.length == 0 || secondList.length == 0) return new int[][]{};

    int currentAInterval = 0, currentBInterval = 0;
    List<int[]> intersections = new ArrayList<>();

    while(currentAInterval < firstList.length && currentBInterval < secondList.length){
        int[] intervalA = firstList[currentAInterval], intervalB = secondList[currentBInterval];

        if(intervalA[1] >= intervalB[0] || intervalB[1] >= intervalA[0]){
          int start = Math.max(intervalA[0], intervalB[0]);
          int end = Math.min(intervalA[1], intervalB[1]);
          if(end >= start){
              intersections.add(new int[]{start, end});
          }
        }

        if(intervalA[1] > intervalB[1]){
          ++currentBInterval;
        }else if(intervalA[1] < intervalB[1]){
          ++currentAInterval;
        }else{
          ++currentAInterval;
          ++currentBInterval;
        }
    }

    return intersections.toArray(new int[intersections.size()][]);
}

/**
 * @param {number[][]} firstList
 * @param {number[][]} secondList
 * @return {number[][]}
 */
var intervalIntersection = function (firstList, secondList) {
  if (firstList.length === 0 || secondList.length === 0) return [];

  let currentAInterval = 0;
  let currentBInterval = 0;
  const intersections = [];

  while (
    currentAInterval < firstList.length &&
    currentBInterval < secondList.length
  ) {
    const intervalA = firstList[currentAInterval];
    const intervalB = secondList[currentBInterval];

    if (intervalA[1] >= intervalB[0] || intervalB[1] >= intervalA[0]) {
      const start = Math.max(intervalA[0], intervalB[0]);
      const end = Math.min(intervalA[1], intervalB[1]);
      if (end >= start) {
        intersections.push([start, end]);
      }
    }

    if (intervalA[1] > intervalB[1]) {
      currentBInterval++;
    } else if (intervalA[1] < intervalB[1]) {
      currentAInterval++;
    } else {
      currentAInterval++;
      currentBInterval++;
    }
  }

  return intersections;
};

class Solution:
    def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
        if len(firstList) == 0 or len(secondList) == 0:
            return []

        currentAInterval = 0
        currentBInterval = 0
        intersections = []

        while currentAInterval < len(firstList) and currentBInterval < len(secondList):
            intervalA = firstList[currentAInterval]
            intervalB = secondList[currentBInterval]

            if intervalA[1] >= intervalB[0] or intervalB[1] >= intervalA[0]:
                start = max(intervalA[0], intervalB[0])
                end = min(intervalA[1], intervalB[1])
                if end >= start:
                    intersections.append([start, end])

            if intervalA[1] > intervalB[1]:
                currentBInterval += 1
            elif intervalA[1] < intervalB[1]:
                currentAInterval += 1
            else:
                currentAInterval += 1
                currentBInterval += 1

        return intersections

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
        if (firstList.empty() || secondList.empty()) {
            return {};
        }

        int currentAInterval = 0;
        int currentBInterval = 0;
        std::vector<std::vector<int>> intersections;

        while (currentAInterval < firstList.size() && currentBInterval < secondList.size()) {
            std::vector<int>& intervalA = firstList[currentAInterval];
            std::vector<int>& intervalB = secondList[currentBInterval];

            if (intervalA[1] >= intervalB[0] || intervalB[1] >= intervalA[0]) {
                int start = std::max(intervalA[0], intervalB[0]);
                int end = std::min(intervalA[1], intervalB[1]);
                if (end >= start) {
                    intersections.push_back({start, end});
                }
            }

            if (intervalA[1] > intervalB[1]) {
                ++currentBInterval;
            } else if (intervalA[1] < intervalB[1]) {
                ++currentAInterval;
            } else {
                ++currentAInterval;
                ++currentBInterval;
            }
        }

        return intersections;
    }
};

Time/Space Complexity:

Time Complexity: O(min(m, n)) where m is the length of firstList and n lenght of secondList
Space Complexity: O(1)

Explanation:

Note that we don't need extra space since we only use the intersections for storing the result. It's similar to the merging of two sorted linked list as we saw in Merge Two Sorted Lists. We have the pointers to the first intervals in both lists, and we iterate over both list of intervals until we hit end of the smaller list (or both if they're of equal length). Each time we check if the two currently selected intervals have any intersections by comparing their start and end times (e.g. if intervalA[1] >= intervalB[0] that means there might an overlap since the intervalA end time might be between intervalB start and end time, we make sure that's true with end >= start, also same logic goes if the intervalB end time is between intervalA start and end time). We choose the start and end of the intersection interval by choosing the maximum start of two intersecting intervals, and minimum end time. We check if it makes sense to keep the currently chosen intervals for next iteration by checking their end time (e.g if intervalA[1] > intervalB[1] means that intervalB has elapsed, so we check if we can combine current intervalA with the next interval intervalB in the secondList). The time complexity is time required to loop over the smaller list.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​