Skip to main content

Word Search II

Word Search II: Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:​

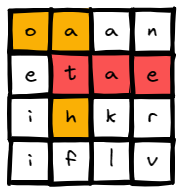
image

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]],
words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]
Example 2:​

image

Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []
Constraints:​
  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 12
  • board[i][j] is a lowercase English letter.
  • 1 <= words.length <= 3 * 10^4
  • 1 <= words[i].length <= 10
  • words[i] consists of lowercase English letters.
  • All the strings of words are unique.

Try this Problem on your own or check similar problems:

  1. Word Search
  2. Unique Paths III
  3. Encrypt and Decrypt Strings
Solution:​
class Solution {
    class Trie {
      public class TrieNode{
        TrieNode[] children;
        boolean isWord = false;
        String word;
        public TrieNode(){
          children = new TrieNode[26];
        }
      }

      TrieNode root;
      public Trie() {
        root = new TrieNode();
      }

      public void insert(String word) {
        TrieNode iter = root;
        for(int i = 0; i < word.length(); ++i){
          char letter = word.charAt(i);
          if(iter.children[letter - 'a'] == null){
            iter.children[letter - 'a'] = new TrieNode();
          }
          iter = iter.children[letter - 'a'];
        }
        iter.isWord = true;
        iter.word = word;
      }
    }

    public List<String> findWords(char[][] board, String[] words) {
      Trie trie = new Trie();
      List<String> result = new ArrayList<>();

      for(String word: words){
        trie.insert(word);
      }

      for(int i = 0; i < board.length; ++i){
        for(int j = 0; j < board[0].length; ++j){
          helper(board, i, j, trie.root, result);
        }
      }
      return result;
    }

    private void helper(char[][] board, int x, int y, Trie.TrieNode root, List<String> result){
      if(x < 0 || x == board.length || y < 0 || y == board[0].length || board[x][y] == '#' || root.children[board[x][y] - 'a'] == null){
        return;
      }

      char c = board[x][y];
      root = root.children[c - 'a'];
      if(root.isWord){
        result.add(root.word);
        root.isWord = false;
      }

      board[x][y] = '#';

      helper(board, x + 1, y, root, result);
      helper(board, x, y + 1, root, result);
      helper(board, x - 1, y, root, result);
      helper(board, x, y - 1, root, result);

      board[x][y] = c;
    }
}
Time/Space Complexity:​
  • Time Complexity: O(mn4^L) where L is the average/maximum length of a word in input array words
  • Space Complexity: O(sum(w) + L) sum(w) for the trie, and L for the maximum recursion stack while searching for words
Explanation:​

We combine two approach Word Search (we also get the same time complexity because of trie) and Trie like in Implement Trie (Prefix Tree) or Longest Word in Dictionary (making the space complexity sum of all word lengths since we're holding all words in each word-ending node in the trie). There are a few tricks we have to add to make the solution functional:

  • Note we're using TrieNode to keep on expanding the current word candidate instead of having a StringBuilder or string. This is way better option, since we can easily check if current word candidate is a prefix of any inserted word in trie root.children[board[x][y] - 'a'] == null (we're basically pruning the search)
  • Just like in Word Search we have special character '#' so that we don't have to create a visited matrix
  • Note that different paths can lead to same words, so to remove duplicates one way is to use a Set, but we can again utilize the Trie and once we have found a word in the board, we do the deduplication in the trie by changing the flag root.isWord = false;. Next time we find the same word, the flag isWord will be false so we will not add it in the result.