N-Queens
N-Queens:
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
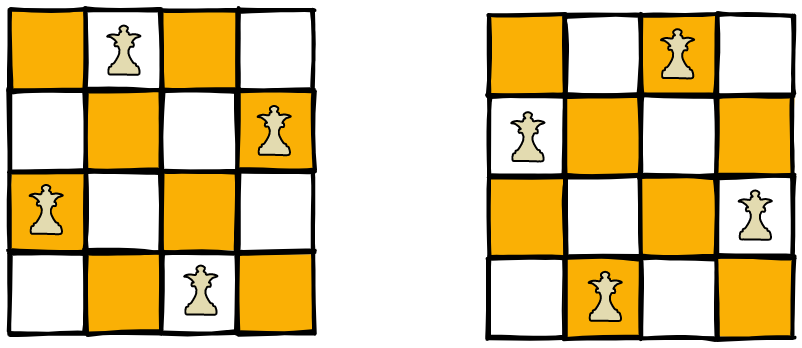
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1
Output: [["Q"]]
Constraints:
1 <= n <= 9
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> result = new ArrayList<>();
char[][] board = new char[n][n];
for(int i = 0; i < n; ++i){
Arrays.fill(board[i], '.');
}
helper(board, 0, n, result);
return result;
}
private void helper(char[][] board, int row, int n, List<List<String>> result){
if(row == n){
List<String> configuration = new ArrayList<>();
for(int i = 0; i < n; ++i){
configuration.add(new String(board[i]));
}
result.add(configuration);
return;
}
for(int i = 0; i < n; ++i){
if(isValidPlacement(board, row, i)){
board[row][i] = 'Q';
helper(board, row + 1, n, result);
board[row][i] = '.';
}
}
}
private boolean isValidPlacement(char[][] board, int row, int column){
for(int i = 0; i < row; ++i){
if(board[i][column] != '.') return false;
}
for(int i = row - 1, j = column - 1; i >= 0 && j >= 0; --i, --j){
if(board[i][j] != '.') return false;
}
for(int i = row - 1, j = column + 1; i >= 0 && j < board.length; --i, ++j){
if(board[i][j] != '.') return false;
}
return true;
}
}
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function (n) {
const result = [];
const board = Array.from({ length: n }, () => Array(n).fill("."));
helper(board, 0, n, result);
return result;
};
function helper(board, row, n, result) {
if (row === n) {
const configuration = board.map((row) => row.join(""));
result.push(configuration);
return;
}
for (let col = 0; col < n; col++) {
if (isValidPlacement(board, row, col)) {
board[row][col] = "Q";
helper(board, row + 1, n, result);
board[row][col] = ".";
}
}
}
function isValidPlacement(board, row, col) {
const n = board.length;
for (let i = 0; i < row; i++) {
if (board[i][col] === "Q") {
return false;
}
}
for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] === "Q") {
return false;
}
}
for (let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board[i][j] === "Q") {
return false;
}
}
return true;
}
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
result = []
board = [['.' for _ in range(n)] for _ in range(n)]
self.helper(board, 0, n, result)
return result
def helper(self, board: List[List[str]], row: int, n: int, result: List[List[str]]) -> None:
if row == n:
configuration = [''.join(row) for row in board]
result.append(configuration)
return
for col in range(n):
if self.isValidPlacement(board, row, col):
board[row][col] = 'Q'
self.helper(board, row + 1, n, result)
board[row][col] = '.'
def isValidPlacement(self, board: List[List[str]], row: int, col: int) -> bool:
n = len(board)
for i in range(row):
if board[i][col] == 'Q':
return False
for i, j in zip(range(row - 1, -1, -1), range(col - 1, -1, -1)):
if board[i][j] == 'Q':
return False
for i, j in zip(range(row - 1, -1, -1), range(col + 1, n)):
if board[i][j] == 'Q':
return False
return True
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
std::vector<std::vector<std::string>> result;
std::vector<std::vector<char>> board(n, std::vector<char>(n, '.'));
helper(board, 0, n, result);
return result;
}
private:
void helper(std::vector<std::vector<char>>& board, int row, int n, std::vector<std::vector<std::string>>& result) {
if (row == n) {
std::vector<std::string> configuration;
for (int i = 0; i < n; ++i) {
configuration.push_back(std::string(board[i].begin(), board[i].end()));
}
result.push_back(configuration);
return;
}
for (int i = 0; i < n; ++i) {
if (isValidPlacement(board, row, i)) {
board[row][i] = 'Q';
helper(board, row + 1, n, result);
board[row][i] = '.';
}
}
}
bool isValidPlacement(const std::vector<std::vector<char>>& board, int row, int column) {
for (int i = 0; i < row; ++i) {
if (board[i][column] != '.') return false;
}
for (int i = row - 1, j = column - 1; i >= 0 && j >= 0; --i, --j) {
if (board[i][j] != '.') return false;
}
for (int i = row - 1, j = column + 1; i >= 0 && j < board.size(); --i, ++j) {
if (board[i][j] != '.') return false;
}
return true;
}
};
Time/Space Complexity:
- Time Complexity: O(n*n!)
- Space Complexity: O(n^2)
Explanation:
We keep a board which is a array of arrays of characters as a helper data structure leading to O(n^2) space complexity, while for time complexity at each level we have one less option than at the level before (n * (n-1) * (n-2)... * 1 = n!) with a multiplier of n (because of for loop in base case) leading to n * n!. We first fill the board with empty cells marked with '.', then we call our recursive function helper which takes as parameter current row where we're trying to place the queen. If we have reached n rows we have a valid configuration which we add to our result list which will be later returned as final result from the main function. Otherwise, we try to place the queen in the current row, by trying all columns and checking with isValidPlacement function if we can place it at each of the columns. If we can place it, we mark the cell with 'Q' and try to solve the board with this selection by moving to the next row, finally we backtrack board[row][i] = '.'; so we can choose another column. The validation function first check if we have a queen in the same column as our current placement selection, and it returns false as validation result if we do. The same goes for the left and right diagonal check (the last two for loops), otherwise if there isn't a queen on the board attacking our selected cell, we return true.