Maximal Square

Maximal Square: Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

Example 1:

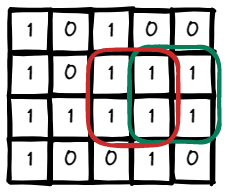
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],
["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] is '0' or '1'.

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

class Solution {
  public int maximalSquare(char[][] matrix) {
      int maxLength = 0, m = matrix.length, n = matrix[0].length;
      int[][] dp = new int[m][n];

      for(int i = 0;  i < m; ++i){
          if(matrix[i][0] == '1'){
              dp[i][0] = 1;
              maxLength = 1;
          }
      }
      for(int i = 0;  i < n; ++i){
          if(matrix[0][i] == '1'){
              dp[0][i] = 1;
              maxLength = 1;
          }
      }

      for(int i = 1; i < m; ++i){
          for(int j = 1; j < n; ++j){
              if(matrix[i][j] != '0'){
                  dp[i][j] = Math.max(Math.min(dp[i][j-1], Math.min(dp[i-1][j], dp[i-1][j-1])) + 1, dp[i][j]);
                  maxLength = Math.max(maxLength, dp[i][j]);
              }
          }
      }

      return maxLength * maxLength;
  }
}

/**
 * @param {character[][]} matrix
 * @return {number}
 */
var maximalSquare = function (matrix) {
  let maxLength = 0;
  const m = matrix.length;
  const n = matrix[0].length;
  const dp = Array.from({ length: m }, () => Array(n).fill(0));

  for (let i = 0; i < m; ++i) {
    if (matrix[i][0] === "1") {
      dp[i][0] = 1;
      maxLength = 1;
    }
  }
  for (let i = 0; i < n; ++i) {
    if (matrix[0][i] === "1") {
      dp[0][i] = 1;
      maxLength = 1;
    }
  }

  for (let i = 1; i < m; ++i) {
    for (let j = 1; j < n; ++j) {
      if (matrix[i][j] !== "0") {
        dp[i][j] = Math.max(
          Math.min(dp[i][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j - 1])) + 1,
          dp[i][j]
        );
        maxLength = Math.max(maxLength, dp[i][j]);
      }
    }
  }

  return maxLength * maxLength;
};

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        maxLength = 0
        m, n = len(matrix), len(matrix[0])
        dp = [[0] * n for _ in range(m)]

        for i in range(m):
            if matrix[i][0] == '1':
                dp[i][0] = 1
                maxLength = 1
        for i in range(n):
            if matrix[0][i] == '1':
                dp[0][i] = 1
                maxLength = 1

        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] != '0':
                    dp[i][j] = max(
                        min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1, dp[i][j]
                    )
                    maxLength = max(maxLength, dp[i][j])

        return maxLength * maxLength

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int maxLength = 0;
        int m = matrix.size();
        int n = matrix[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));

        for (int i = 0; i < m; ++i) {
            if (matrix[i][0] == '1') {
                dp[i][0] = 1;
                maxLength = 1;
            }
        }
        for (int i = 0; i < n; ++i) {
            if (matrix[0][i] == '1') {
                dp[0][i] = 1;
                maxLength = 1;
            }
        }

        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][j] != '0') {
                    dp[i][j] = max(min(dp[i][j - 1], min(dp[i - 1][j], dp[i - 1][j - 1])) + 1, dp[i][j]);
                    maxLength = max(maxLength, dp[i][j]);
                }
            }
        }

        return maxLength * maxLength;
    }
};

Time/Space Complexity:

Time Complexity: O(nm)
Space Complexity: O(nm)

Explanation:

We traverse the whole matrix while also keeping the track of maximum length of square for each cell in dp matrix of the same size as input leading to O(mn) space and time complexity. We first check if we can at least form a square of one 1 cell in the first column and first row. We also initialize our dp with 1 if the cell in matrix is 1. Next we traverse the matrix and for each cell we check if it's 1, and we check the minimum length for its 3 surrounding cells (dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) which now form a square. If all cells form a square of length 2 we can now form even bigger square of length 3 since we have the one 1 in the current cell and we know that it's forming a row and column of 1 with dp[i][j-1] and dp[i-1][j], and that we have a square of 2x2 in dp[i-1][j-1]. For each cell we check if we find a larger square by recording its length which we finally return as our result (we return square area made with that length). We could reduce the space complexity to O(n) since for the calculation we only need the previous row which we can get with current value of dp[j], we need dp[i-1][j-1] so we record it using temp to store it before computation and save it into prev. We also need dp[i][j-1] which we can easily get with dp[j-1]. Note that we offset the dp with 1, so we don't encounter out-of-boundary problems with dp[j-1] if we start with j = 0.

Java
JavaScript
Python
C++

public int maximalSquare(char[][] matrix) {
    int m = matrix.length, n = matrix[0].length;
    int[] dp = new int[n + 1];
    int maxLength = 0, prev = 0;

    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            int temp = dp[j];
            if (matrix[i - 1][j - 1] != '0') {
                dp[j] = Math.min(dp[j-1], Math.min(dp[j], prev)) + 1;
                maxLength = Math.max(maxLength, dp[j]);
            } else {
                dp[j] = 0;
            }
            prev = temp;
        }
    }
    return maxLength * maxLength;
}

/**
 * @param {character[][]} matrix
 * @return {number}
 */
var maximalSquare = function (matrix) {
  const m = matrix.length;
  const n = matrix[0].length;
  const dp = new Array(n + 1).fill(0);
  let maxLength = 0;
  let prev = 0;

  for (let i = 1; i <= m; ++i) {
    for (let j = 1; j <= n; ++j) {
      const temp = dp[j];
      if (matrix[i - 1][j - 1] !== "0") {
        dp[j] = Math.min(dp[j - 1], Math.min(dp[j], prev)) + 1;
        maxLength = Math.max(maxLength, dp[j]);
      } else {
        dp[j] = 0;
      }
      prev = temp;
    }
  }
  return maxLength * maxLength;
};

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m = len(matrix)
        n = len(matrix[0])
        dp = [0] * (n + 1)
        maxLength = 0
        prev = 0

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                temp = dp[j]
                if matrix[i - 1][j - 1] != '0':
                    dp[j] = min(dp[j - 1], min(dp[j], prev)) + 1
                    maxLength = max(maxLength, dp[j])
                else:
                    dp[j] = 0
                prev = temp

        return maxLength * maxLength

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<int> dp(n + 1, 0);
        int maxLength = 0;
        int prev = 0;

        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                int temp = dp[j];
                if (matrix[i - 1][j - 1] != '0') {
                    dp[j] = min(dp[j - 1], min(dp[j], prev)) + 1;
                    maxLength = max(maxLength, dp[j]);
                } else {
                    dp[j] = 0;
                }
                prev = temp;
            }
        }
        return maxLength * maxLength;
    }
};

Example 1:​

Example 2:​

Example 3:​

Constraints:​

Solution:​

Time/Space Complexity:​

Explanation:​