Skip to main content

Maximum Profit in Job Scheduling

Maximum Profit in Job Scheduling: We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:​

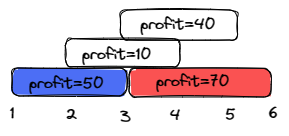
image

Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job.
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2:​

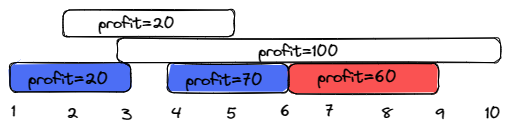
image

Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job.
Profit obtained 150 = 20 + 70 + 60.
Example 3:​

image

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6
Constraints:​
  • 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
  • 1 <= startTime[i] < endTime[i] <= 10^9
  • 1 <= profit[i] <= 10^4

Try this Problem on your own or check similar problems:

  1. Two Best Non-Overlapping Events
  2. Maximum Earnings From Taxi
Solution:​
class Solution {
  public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
      int[][] jobs = new int[startTime.length][3];
      for (int i = 0; i < startTime.length; ++i) {
          jobs[i] = new int[]{startTime[i], endTime[i], profit[i]};
      }
      Arrays.sort(jobs, (a, b) -> a[0] - b[0]);

      int[] dp = new int[jobs.length];
      dp[jobs.length - 1] = jobs[jobs.length - 1][2];

      for (int i = jobs.length - 2; i >= 0; --i) {
          int next = nextJob(jobs, i);
          dp[i] = Math.max(jobs[i][2] + (next == -1 ? 0 : dp[next]), dp[i + 1]);
      }

      return dp[0];
  }

  private int nextJob(int[][] jobs, int index){
      int start = index + 1;
      int end = jobs.length - 1;
      while(start <= end) {
          int mid = start + (end - start) / 2;
          if(jobs[mid][0] >= jobs[index][1]) {
              if(jobs[mid-1][0] >= jobs[index][1])
                end = mid - 1;
              else
                return mid;
          } else {
              start = mid + 1;
          }
      }
      return -1;
  }
}
Time/Space Complexity:​
  • Time Complexity: O(nlogn)
  • Space Complexity: O(n)
Explanation:​

We're creating job triples (start, end, profit) by combining the values from the three input arrays and we also have dp tracking the current max profit for each job, so we have linear space complexity proportional to the number of jobs. We sort the jobs by start time, leading to O(nlogn) time complexity, for each job we also do a binary search to find the next not-overlapping job leading again to O(nlogn) time complexity. How do we make decision to take or not to take the job (0/1 Knapsack problem), well we can start with the last job, we know that maximum profit if no other job is available is the profit of the current job so we initialize dp[jobs.length - 1] = jobs[jobs.length - 1][2]. Now for each of the jobs traversing backwards we try to optimize by either:

  • Taking the current job profit and the maximum profit earned from the next non-overlapping job.
  • We don't take the job, so the maximum is the maximum profit earned starting from the next job i+1.

Each time we make a decision that maximizes the profit. Finally dp[0] will contain the maximum profit we can earn by either taking the first job or not taking it and getting the maximum from a combination of other jobs. The next question is how do we find the next non-overlapping job? Since the array containing all jobs is sorted, we can utilize the binary search, for each mid we compare if the start of it is passed (or at the same time) the end of the current job. If it isn't we know that we must move deeper into the array, where we have larger start jobs, however if it is we check is it really the first non-overlapping job (by checking for mid-1). If it is we return the mid, but if it's not we know that the right half of binary search is useless for us to search in, since we know we have a better candidate at mid-1, so we eliminate the second half of binary search. Note also that mid can range from index + 1 to jobs.length - 1, so checking for mid - 1 will not cause out of boundary error, since we're always starting our search from the index+1 and we know that the minimum passed index will be 0.

The solution given in the Section uses the bottom-up (tabulation) dp, for completion’s sake we also implement the top-down (memoization) approach:

class Solution {
    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        int[][] jobs = new int[startTime.length][3];
        Map<Integer, Integer> dp = new HashMap<>();

        for (int i = 0; i < startTime.length; ++i) {
            jobs[i] = new int[]{startTime[i], endTime[i], profit[i]};
        }
        Arrays.sort(jobs, (a, b) -> a[0] - b[0]);

        return helper(jobs, 0, dp);
    }

    public int helper(int[][] jobs, int job, Map<Integer, Integer> dp){
        if(job == jobs.length) return 0;

        if(dp.containsKey(job)) return dp.get(job);

        int next = nextJob(jobs, job);
        int withCurrentJob = jobs[job][2] + (next != -1 ? helper(jobs, next, dp) : 0);
        int withoutCurrentJob = helper(jobs, job + 1, dp);

        int maxProfit = Math.max(withCurrentJob, withoutCurrentJob);
        dp.put(job, maxProfit);
        return maxProfit;
    }

    private int nextJob(int[][] jobs, int index){
        int start = index + 1;
        int end = jobs.length - 1;
        while(start <= end) {
            int mid = start + (end - start) / 2;
            if(jobs[mid][0] >= jobs[index][1]) {
                if(jobs[mid-1][0] >= jobs[index][1])
                    end = mid - 1;
                else
                    return mid;
            } else {
                start = mid + 1;
            }
        }
        return -1;
    }

}