Container With Most Water

---

Container With Most Water: You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

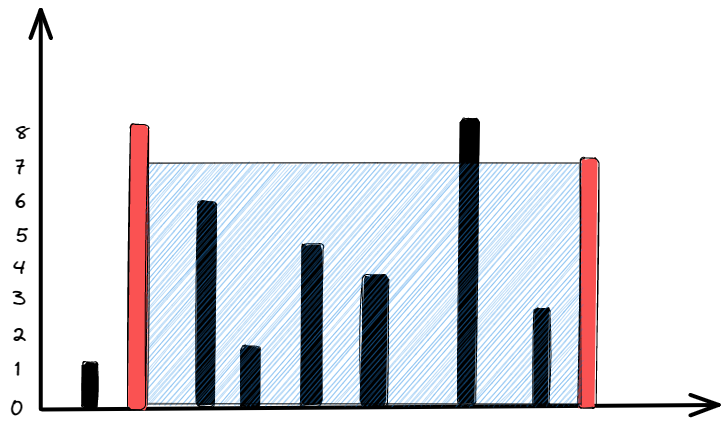
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7].
In this case, the max area of water (blue section) the container can contain is 49.

---

Example 2:

Input: height = [1,1]
Output: 1

---

Constraints:

• n == height.length
• 2 <= n <= 10^5
• 0 <= height[i] <= 10^4

---

Try this Problem on your own or check similar problems:

1. Maximum Tastiness of Candy Basket
2. Trapping Rain Water

Solution:

Java

public int maxArea(int[] height) {
  int i = 0, j = height.length - 1, maxAmount = 0;
  while(i < j){
      maxAmount = Math.max(maxAmount, (j - i) * Math.min(height[i], height[j]));
      if(height[i] < height[j]){
        ++i;
      }else if(height[i] > height[j]){
        --j;
      }else{
        ++i;
        --j;
      }
  }

  return maxAmount;
}

JavaScript

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function (height) {
  let i = 0;
  let j = height.length - 1;
  let maxAmount = 0;

  while (i < j) {
    maxAmount = Math.max(maxAmount, (j - i) * Math.min(height[i], height[j]));

    if (height[i] < height[j]) {
      ++i;
    } else if (height[i] > height[j]) {
      --j;
    } else {
      ++i;
      --j;
    }
  }

  return maxAmount;
};

Python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        i = 0
        j = len(height) - 1
        max_amount = 0

        while i < j:
            max_amount = max(max_amount, (j - i) * min(height[i], height[j]))

            if height[i] < height[j]:
                i += 1
            elif height[i] > height[j]:
                j -= 1
            else:
                i += 1
                j -= 1

        return max_amount

C++

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0;
        int j = height.size() - 1;
        int maxAmount = 0;

        while (i < j) {
            maxAmount = max(maxAmount, (j - i) * min(height[i], height[j]));

            if (height[i] < height[j]) {
                ++i;
            } else if (height[i] > height[j]) {
                --j;
            } else {
                ++i;
                --j;
            }
        }

        return maxAmount;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(1)

---

Explanation:

We have a linear time complexity since we have to traverse the input height array only once. To maximize the amount of water we want to maximize the width between the start and end, and the height of each of the boundaries at the start and end. So, we start with the maximum width, two pointers each side of the input array, the total amount of water we can hold is equal to the product of the width and the lower height of two boundaries (so that we don't spill the water). For every pair of boundaries, we check if they can hold more water than the amount, we recorded to be the maximum up until that point maxAmount. But how do we shift the boundaries for each of the iterations? We have three scenarios:

• The height of the beginning of the boundary is smaller than the height of the end, so we move to the right ++i so we can find a closer match to the end boundary (increase the height at the cost of decreasing the width).
• Or we can have it the other way around the end is smaller than the beginning, so we move it to the left to find a better match.
• The heights are the same, so we can't really find a boundary that can hold more water by decreasing the width (since at this point this is the maximum water we can hold for these heights), so we move the start of boundary to the right, and the end of boundary to the left, hoping to find larger heights at the cost of having smaller widths.