Trapping Rain Water

---

Trapping Rain Water: Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

Example 1:

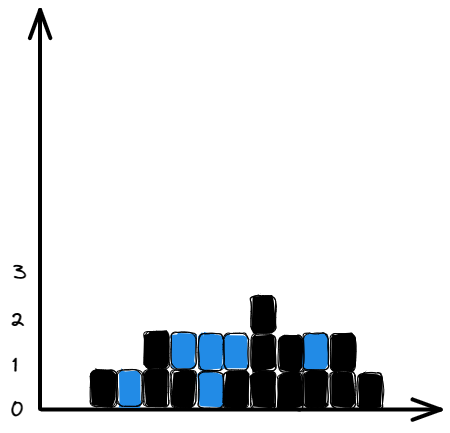
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section)
is represented by array [0,1,0,2,1,0,1,3,2,1,2,1].
In this case, 6 units of rain water (blue section) are being trapped.

---

Example 2:

Input: height = [4,2,0,3,2,5]
Output: 9

---

Constraints:

• n == height.length
• 1 <= n <= 2 * 10^4
• 0 <= height[i] <= 10^5

---

Try this Problem on your own or check similar problems:

1. Container With Most Water
2. Product of Array Except Self
3. Trapping Rain Water II

Solution:

Java

public int trap(int[] height) {
    int waterTrapped = 0;
    int left = 0, right = height.length - 1;
    int maxLeft = Integer.MIN_VALUE, maxRight = Integer.MIN_VALUE;

    while(left < right){
        if(height[left] > maxLeft){
            maxLeft = height[left];
        }
        if(height[right] > maxRight){
            maxRight = height[right];
        }

        if(height[left] < height[right]){
            waterTrapped += maxLeft - height[left];
            ++left;
        }else{
            waterTrapped += maxRight - height[right];
            --right;
        }
    }

    return waterTrapped;
}

JavaScript

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  let waterTrapped = 0;
  let left = 0;
  let right = height.length - 1;
  let maxLeft = -Infinity;
  let maxRight = -Infinity;

  while (left < right) {
    if (height[left] > maxLeft) {
      maxLeft = height[left];
    }
    if (height[right] > maxRight) {
      maxRight = height[right];
    }

    if (height[left] < height[right]) {
      waterTrapped += maxLeft - height[left];
      left += 1;
    } else {
      waterTrapped += maxRight - height[right];
      right -= 1;
    }
  }

  return waterTrapped;
};

Python

class Solution:
    def trap(self, height: List[int]) -> int:
        waterTrapped = 0
        left = 0
        right = len(height) - 1
        maxLeft = float('-inf')
        maxRight = float('-inf')

        while left < right:
            if height[left] > maxLeft:
                maxLeft = height[left]
            if height[right] > maxRight:
                maxRight = height[right]

            if height[left] < height[right]:
                waterTrapped += maxLeft - height[left]
                left += 1
            else:
                waterTrapped += maxRight - height[right]
                right -= 1

        return waterTrapped

C++

class Solution {
public:
    int trap(vector<int>& height) {
        int waterTrapped = 0;
        int left = 0;
        int right = height.size() - 1;
        int maxLeft = INT_MIN;
        int maxRight = INT_MIN;

        while (left < right) {
            if (height[left] > maxLeft) {
                maxLeft = height[left];
            }
            if (height[right] > maxRight) {
                maxRight = height[right];
            }

            if (height[left] < height[right]) {
                waterTrapped += maxLeft - height[left];
                left += 1;
            } else {
                waterTrapped += maxRight - height[right];
                right -= 1;
            }
        }

        return waterTrapped;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(1)

---

Explanation:

To determine if we can hold water in certain elevation, that elevation has to be bound by both sides. For example, if we take the first half and we already know the maximum elevation on that side how can we be sure we can hold the water? Well first if the maximum elevation comes before the current elevation, we can be sure that we're bound by one side, but what about the other side? We use the two pointers approach and place the pointers on each side of the input array, now if we the current elevation left pointer is pointing to is smaller than the elevation right is pointing to, we can be sure that elevation at left is bounded by elevation at right. Using that together with fact that left elevation is also bound by the current max elevation in the left half, we know we have elevation that can hold water, the question is how much water? Well, it's the difference between maxLeft and current elevation left is pointing to. The same logic applies if we're assuming right elevation is smaller than the left elevation. Using these ideas, we arrive at linear time complexity algorithm.