Search a 2D Matrix

---

Search a 2D Matrix: Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

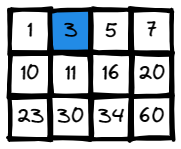
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

---

Example 2:

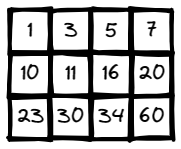
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

---

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

---

Try this Problem on your own or check similar problems:

1. Search a 2D Matrix II
2. Split Message Based on Limit

Solution:

Java

public boolean searchMatrix(int[][] matrix, int target) {
    int m = matrix.length, n = matrix[0].length, start = 0, end = m * n - 1;

    while(start <= end){
        int mid = start + (end - start) / 2;
        int row = mid / n, column = mid % n;
        if(matrix[row][column] == target) return true;
        else if(matrix[row][column] < target) start = mid + 1;
        else end = mid - 1;
    }

    return false;
}

JavaScript

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
  const m = matrix.length;
  const n = matrix[0].length;
  let start = 0;
  let end = m * n - 1;

  while (start <= end) {
    const mid = start + Math.floor((end - start) / 2);
    const row = Math.floor(mid / n);
    const column = mid % n;

    if (matrix[row][column] === target) {
      return true;
    } else if (matrix[row][column] < target) {
      start = mid + 1;
    } else {
      end = mid - 1;
    }
  }

  return false;
};

Python

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
      m = len(matrix)
      n = len(matrix[0])
      start = 0
      end = m * n - 1

      while start <= end:
          mid = start + (end - start) // 2
          row = mid // n
          column = mid % n

          if matrix[row][column] == target:
              return True
          elif matrix[row][column] < target:
              start = mid + 1
          else:
              end = mid - 1

      return False

C++

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        int n = matrix[0].size();
        int start = 0;
        int end = m * n - 1;

        while (start <= end) {
            int mid = start + (end - start) / 2;
            int row = mid / n;
            int column = mid % n;

            if (matrix[row][column] == target) {
                return true;
            } else if (matrix[row][column] < target) {
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }

        return false;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(log(m*n))
• Space Complexity: O(1)

---

Explanation:

The implementation is the standard binary search but this time it is on a 2D array. Note that 2D array can be flattened to 1D array extracting each row and putting them next to each other, so we treat the search space of 2D array just like we would if we had a 1D array. Our start will be the first element of the matrix, while our end will be the last element of the matrix. The mid represents the index of flatten 2d matrix, the only tricky part is how do we get the correct row and column for the mid element inside matrix? We use int row = mid / n, column = mid % n; just like we did in Convert 1D Array into 2D Array . We use the same straightforward implementation of binary search. Since the size of matrix is m*n once we apply the binary search we will have O(log (mn)).