Search a 2D Matrix II

---

Search a 2D Matrix II: Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Example 1:

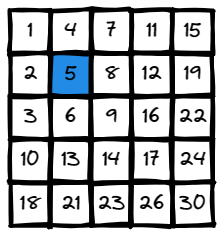
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],
[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

---

Example 2:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],
[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

---

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -10^9 <= matrix[i][j] <= 10^9
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -10^9 <= target <= 10^9

---

Try this Problem on your own or check similar problems:

1. Search a 2D Matrix

Solution:

Java

public boolean searchMatrix(int[][] matrix, int target) {
    int m = matrix.length, n = matrix[0].length;
    int row = 0, column = n - 1;
    while(row < m && column >= 0){
        if(matrix[row][column] == target) return true;
        else if(matrix[row][column] <  target) ++row;
        else --column;
    }
    return false;
}

JavaScript

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
  const m = matrix.length;
  const n = matrix[0].length;
  let row = 0;
  let column = n - 1;

  while (row < m && column >= 0) {
    if (matrix[row][column] === target) {
      return true;
    } else if (matrix[row][column] < target) {
      row++;
    } else {
      column--;
    }
  }

  return false;
};

Python

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m = len(matrix)
        n = len(matrix[0])
        row = 0
        column = n - 1

        while row < m and column >= 0:
            if matrix[row][column] == target:
                return True
            elif matrix[row][column] < target:
                row += 1
            else:
                column -= 1

        return False

C++

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        int n = matrix[0].size();
        int row = 0;
        int column = n - 1;

        while (row < m && column >= 0) {
            if (matrix[row][column] == target) {
                return true;
            } else if (matrix[row][column] < target) {
                ++row;
            } else {
                --column;
            }
        }

        return false;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(m+n)
• Space Complexity: O(1)

---

Explanation:

We use the relatively sorted order in the matrix and start our search from the top right corner. If the current element is equal to target we just return it. Otherwise, if the element is smaller, we know that it's the largest element in that row, so we cannot find our target in that row, and we must go down ++row. If the element is larger than our target, we know that we might find the target in the same row but in a column before the current one, so we go left --column. Finally, if we're out of boundaries and the loop finished, we return false since we couldn't find the target. At most we will loop over one whole row and one whole column (the target is equal to the element in the last row, first column) so the time complexity is bounded by O(m+n).