Cheapest Flights Within K Stops
Cheapest Flights Within K Stops:
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [from_i, to_i, price_i] indicates that there is a flight from city from_i to city to_i with cost price_i.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
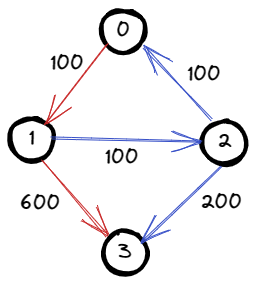
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]],
src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3
is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper
but is invalid because it uses 2 stops.
Example 2:
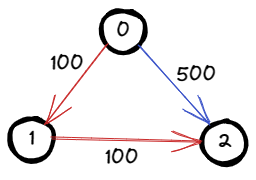
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2
is marked in red and has cost 100 + 100 = 200.
Example 3:
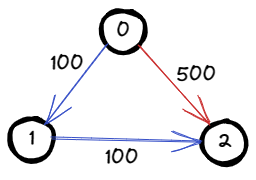
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= from_i, to_i < nfrom_i != to_i1 <= price_i <= 10^4- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
int[] distance = new int[n];
Arrays.fill(distance, Integer.MAX_VALUE);
distance[src] = 0;
for (int i = 0; i <= k; i++) {
int[] temp = Arrays.copyOf(distance, n);
for (int[] flight : flights) {
if (distance[flight[0]] != Integer.MAX_VALUE) {
temp[flight[1]] = Math.min(temp[flight[1]], distance[flight[0]] + flight[2]);
}
}
distance = temp;
}
return distance[dst] == Integer.MAX_VALUE ? -1 : distance[dst];
}
/**
* @param {number} n
* @param {number[][]} flights
* @param {number} src
* @param {number} dst
* @param {number} k
* @return {number}
*/
var findCheapestPrice = function (n, flights, src, dst, k) {
let distance = new Array(n).fill(Infinity);
distance[src] = 0;
for (let i = 0; i <= k; i++) {
const temp = [...distance];
for (const flight of flights) {
if (distance[flight[0]] !== Infinity) {
temp[flight[1]] = Math.min(
temp[flight[1]],
distance[flight[0]] + flight[2]
);
}
}
distance = temp;
}
return distance[dst] === Infinity ? -1 : distance[dst];
};
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
distance = [float('inf')] * n
distance[src] = 0
for i in range(k + 1):
temp = distance.copy()
for flight in flights:
if distance[flight[0]] != float('inf'):
temp[flight[1]] = min(temp[flight[1]], distance[flight[0]] + flight[2])
distance = temp
return -1 if distance[dst] == float('inf') else distance[dst]
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
vector<int> distance(n, numeric_limits<int>::max());
distance[src] = 0;
for (int i = 0; i <= k; i++) {
vector<int> temp(distance);
for (const auto& flight : flights) {
if (distance[flight[0]] != numeric_limits<int>::max()) {
temp[flight[1]] = min(temp[flight[1]], distance[flight[0]] + flight[2]);
}
}
distance = temp;
}
return distance[dst] == numeric_limits<int>::max() ? -1 : distance[dst];
}
};
Time/Space Complexity:
- Time Complexity: O((E+V) * k) where
Eis number of edges/flights,Vis number of vertices/cities - Space Complexity: O(V)
Explanation:
We have linear space complexity proportional to the number of cities (vertices), while for time complexity we repeat the loop k times and we iterate over all edges O(V) and copy over the distance array O(E) so the total time complexity would be O((V+E)*k).
This function finds the shortest path using the Bellman Ford Algorithm. Each iteration we add new edges starting first with our source city and checking if we can optimize (decrease) the price to each of destination cities by flying from it. Since by the problem statement we can only have at maximum k stops, that means that will be looking at maximum path of k+1 edges (e.g. x - a - b - y, k = 2 the stops are a and b, but the path length/number of edges is 3) so by Bellman Ford Algorithm we have to do k+1 relaxations to have a check shortest distance paths up to the length k+1 (that's the reason we iterate 0..k). We also use a temp array so that we don't overwrite the real distance in distance array during the computation. Finally, we check for the minimum distance to our destination city and return it if it's not Integer.MAX_VALUE, otherwise we know there is no path from source to destination and we return -1.
A Bellman-Ford algorithm is also guaranteed to find the shortest path in a graph, similar to Dijkstra’s algorithm. Although Bellman-Ford is slower than Dijkstra’s algorithm, it is capable of handling graphs with negative edge weights, which makes it more versatile. The shortest path cannot be found if there exists a negative cycle in the graph. If we continue to go around the negative cycle an infinite number of times, then the cost of the path will continue to decrease (even though the length of the path is increasing). As a result, Bellman-Ford is also capable of detecting negative cycles, which is an important feature.
The idea behind Bellman Ford Algorithm: The Bellman-Ford algorithm’s primary principle is that it starts with a single source and calculates the distance to each node. The distance is initially unknown and assumed to be infinite, but as time goes on, the algorithm relaxes those paths by identifying a few shorter paths. Hence it is said that Bellman-Ford is based on Principle of Relaxation.
Principle of Relaxation of Edges for Bellman-Ford: It states that for the graph having N vertices, all the edges should be relaxed N-1 times to compute the single source shortest path. In order to detect whether a negative cycle exists or not, relax all the edge one more time and if the shortest distance for any node reduces then we can say that a negative cycle exists. In short if we relax the edges N times, and there is any change in the shortest distance of any node between the N-1th and Nth relaxation than a negative cycle exists, otherwise not exist. Why Relaxing Edges N-1 times, gives us Single Source Shortest Path? In the worst-case scenario, a shortest path between two vertices can have at most N-1 edges, where N is the number of vertices. This is because a simple path in a graph with N vertices can have at most N-1 edges, as it’s impossible to form a closed loop without revisiting a vertex. By relaxing edges N-1 times, the Bellman-Ford algorithm ensures that the distance estimates for all vertices have been updated to their optimal values, assuming the graph doesn’t contain any negative-weight cycles reachable from the source vertex. If a graph contains a negative-weight cycle reachable from the source vertex, the algorithm can detect it after N-1 iterations, since the negative cycle disrupts the shortest path lengths. In summary, relaxing edges N-1 times in the Bellman-Ford algorithm guarantees that the algorithm has explored all possible paths of length up to N-1, which is the maximum possible length of a shortest path in a graph with N vertices. This allows the algorithm to correctly calculate the shortest paths from the source vertex to all other vertices, given that there are no negative-weight cycles.