Clone Graph
Clone Graph: Given a reference of a node in a connected undirected graph.
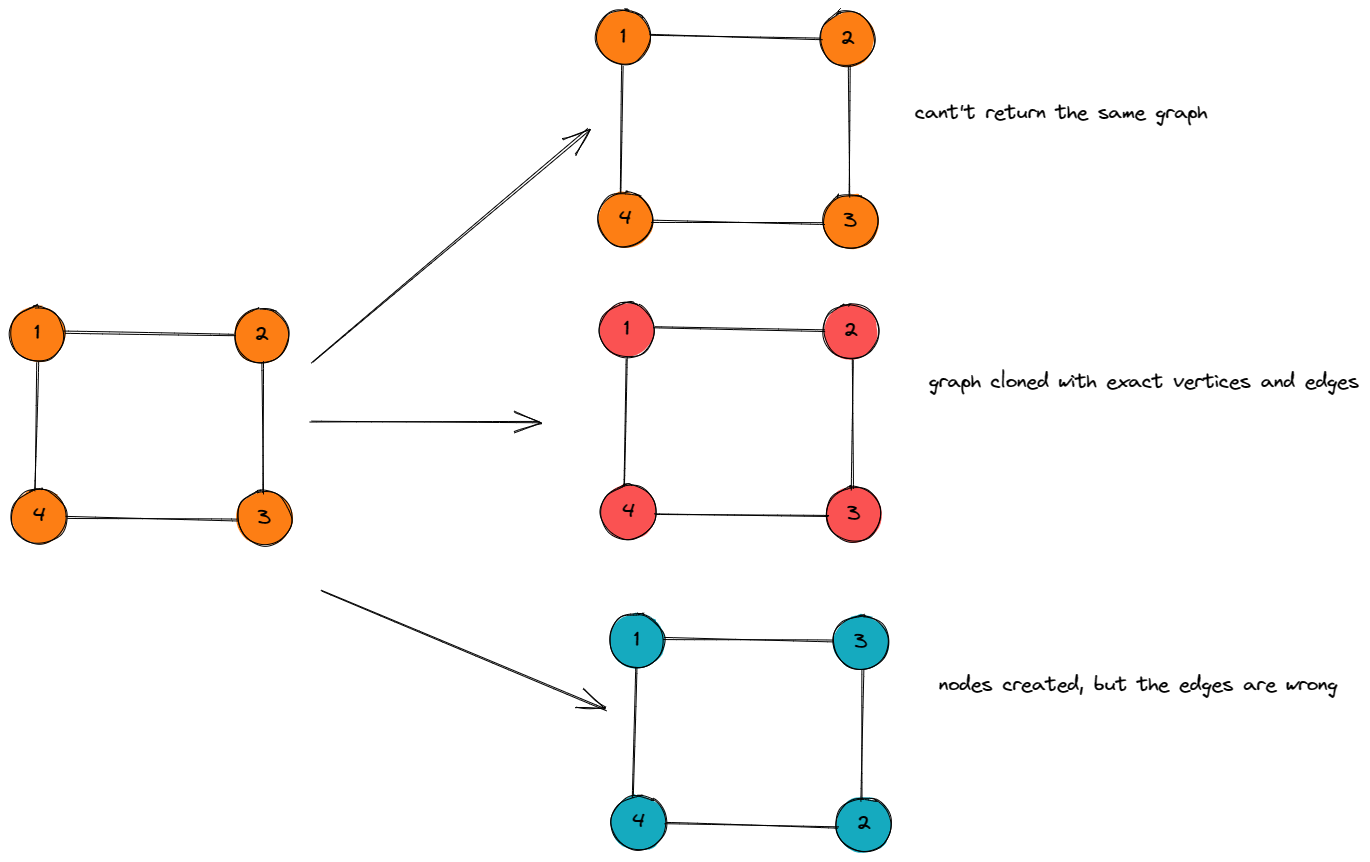
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list.
The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.
Constraints:
- The number of nodes in the graph is in the range
[0, 100]. 1 <= Node.val <= 100Node.valis unique for each node.- There are no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
class Solution {
public Node cloneGraph(Node node) {
if(node == null) return null;
Map<Node, Node> map = new HashMap<>();
map.put(node, new Node(node.val));
Queue<Node> q = new LinkedList<>();
q.add(node);
while(!q.isEmpty()){
Node current = q.poll();
for(Node n: current.neighbors){
if(!map.containsKey(n)){
map.put(n, new Node(n.val));
q.add(n);
}
map.get(current).neighbors.add(map.get(n));
}
}
return map.get(node);
}
}
/**
* // Definition for a Node.
* function Node(val, neighbors) {
* this.val = val === undefined ? 0 : val;
* this.neighbors = neighbors === undefined ? [] : neighbors;
* };
*/
/**
* @param {Node} node
* @return {Node}
*/
var cloneGraph = function (node) {
if (node === null) return null;
const map = new Map();
map.set(node, new Node(node.val));
const queue = [node];
while (queue.length > 0) {
const current = queue.shift();
for (const n of current.neighbors) {
if (!map.has(n)) {
map.set(n, new Node(n.val));
queue.push(n);
}
map.get(current).neighbors.push(map.get(n));
}
}
return map.get(node);
};
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return None
map = {}
map[node] = Node(node.val)
queue = deque([node])
while queue:
current = queue.popleft()
for n in current.neighbors:
if n not in map:
map[n] = Node(n.val)
queue.append(n)
map[current].neighbors.append(map[n])
return map[node]
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
Node* cloneGraph(Node* node) {
if (node == nullptr)
return nullptr;
unordered_map<Node*, Node*> map;
map[node] = new Node(node->val);
queue<Node*> q;
q.push(node);
while (!q.empty()) {
Node* current = q.front();
q.pop();
for (Node* n : current->neighbors) {
if (map.find(n) == map.end()) {
map[n] = new Node(n->val);
q.push(n);
}
map[current]->neighbors.push_back(map[n]);
}
}
return map[node];
}
};
Time/Space Complexity:
- Time Complexity: O(E+V) where
Eis the number of edges andVis the number of vertices/nodes - Space Complexity: O(V)
Explanation:
The first question to ask the interview is if the graph has any self-loops and if we can reach all the nodes by starting from the given input node. As per problem statement we don't have to worry about self-loops, repeating edges and if we can reach any other vertex/node.
We use the BFS approach with a queue to iterate over all vertices in the input graph and each time we encounter a node we don't have in our copy map we add it as key and create a new node as value, we also place it in the queue to be iterated over. The most important line in the code is probably map.get(current).neighbors.add(map.get(n)); in which for the current node of the input graph we find it's clone using our map, and add to the list of its neighbors the current cloned node (neighbor of the node in the original graph). We have to iterate over all edges and vertices so the time complexity is O(E+V) while the space complexity is the number of vertices O(V) (in the cloned map).