Skip to main content

Pacific Atlantic Water Flow

Pacific Atlantic Water Flow: There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.

The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).

The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.

Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.

Example 1:​

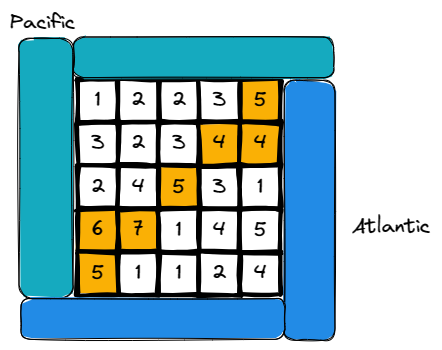
image

Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans,
as shown below:
[0,4]: [0,4] -> Pacific Ocean
       [0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean
       [1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean
       [1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean
       [2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean
       [3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean
       [3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean
       [4,0] -> Atlantic Ocean
Note that there are other possible paths for
these cells to flow to the Pacific and Atlantic oceans.
Example 2:​
Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.
Constraints:​
  • m == heights.length
  • n == heights[r].length
  • 1 <= m, n <= 200
  • 0 <= heights[r][c] <= 10^5

Try this Problem on your own or check similar problems:

  1. Number of Islands
Solution:​
class Solution {
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        List<List<Integer>> result = new ArrayList<>();
        Set<Tuple> atlanticPairs = new HashSet<>(), pacificPairs = new HashSet<>();
        Queue<Tuple> atlanticCandidates = new LinkedList<>(), pacificCandidates = new LinkedList<>();

        for(int i = 0; i < heights.length; ++i){
            Tuple pairFirstColumn = new Tuple(i, 0);
            Tuple pairLastColumn = new Tuple(i, heights[0].length - 1);
            pacificPairs.add(pairFirstColumn);
            atlanticPairs.add(pairLastColumn);
            pacificCandidates.add(pairFirstColumn);
            atlanticCandidates.add(pairLastColumn);
        }


        for(int i = 0; i < heights[0].length; ++i){
            Tuple pairFirstRow = new Tuple(0, i);
            Tuple pairLastRow = new Tuple(heights.length - 1, i);
            pacificPairs.add(pairFirstRow);
            atlanticPairs.add(pairLastRow);
            pacificCandidates.add(pairFirstRow);
            atlanticCandidates.add(pairLastRow);
        }


        bfs(heights, atlanticPairs, atlanticCandidates);
        bfs(heights, pacificPairs, pacificCandidates);

        atlanticPairs.retainAll(pacificPairs);

        return atlanticPairs.stream().map(pair -> List.of(pair.x, pair.y)).collect(Collectors.toList());
    }

    private void bfs(int[][] heights, Set<Tuple> set, Queue<Tuple> q){
        int[][] directions  = new int[][] { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1}};
        int m = heights.length, n = heights[0].length;

        while(!q.isEmpty()){
            Tuple current = q.poll();
            for(int[] d : directions){
                int x = current.x + d[0];
                int y = current.y + d[1];
                Tuple pair = new Tuple(x, y);
                if(x >= 0 && x < m && y >= 0 && y < n &&
                heights[current.x][current.y] <= heights[x][y] && !set.contains(pair)){
                    q.add(pair);
                    set.add(pair);
                }
            }
        }
    }

    class Tuple {
        public int x, y;
        public Tuple(int x, int y) {
            this.x = x;
            this.y = y;
        }
        @Override
        public int hashCode() {
            int hash = 17;
            hash = 31 * hash + this.x;
            hash = 31 * hash + this.y;
            return hash;
        }

        @Override
        public boolean equals(Object other) {
            if (this == other) return true;
            if (other == null) return false;
            if (this.getClass() != other.getClass()) return false;
            Tuple that = (Tuple) other;
            return (this.x == that.x) && (this.y == that.y);
        }
    }
}
Time/Space Complexity:​
  • Time Complexity: O(m*n)
  • Space Complexity: O(m*n)
Explanation:​

There are a lot of moving pieces so let's break down the solution:

  • First, we use the custom class Tuple with overridden hashCode and equals methods so we can create sets with keys of type Tuple
  • We have already implemented BFS a few times, but basically, we have a queue of the candidates we iterate over, and we have a set to check if we have already visited them
  • The neighbors of the current element are defined as per problem statement rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height, which leads to heights[current.x][current.y] <= heights[x][y] requirement when checking the neighbors of the current candidate. We define array of directions to help us navigate to the neighboring cells.
  • In the main function we create two candidate queues, one per ocean, and two sets one per ocean to track elements we have already visited. We fill both the candidate and visited sets with the elements that fulfill the following The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges which leads to adding the first column, first row to pacific candidates/visited set and last column and last row to Atlantic set of candidates.
  • We do BFS on both pairs of candidate/sets and record all elements in the matrix we can reach by placing them in the corresponding set
  • We do the intersection of sets with retainAll which leads us to a modified set containing only cells that are present in both atlantic and pacific visited sets
  • Finally, we use streams to map from set of pairs to list of lists and return it as our result

We iterate over all elements and also can hold reference to all the elements in matrix (all elements reachable and stored in sets) leading to O(m*n) time and space complexity.