Minimum Height Trees

Minimum Height Trees: A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [a_i, b_i] indicates that there is an undirected edge between the two nodes a_i and b_i in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

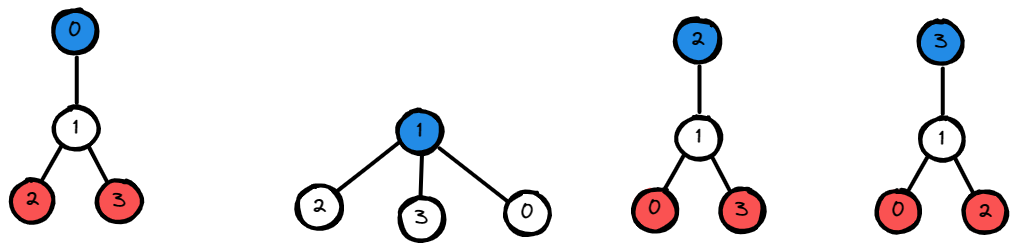
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1
when the root is the node with label 1 which is the only MHT.

Example 2:

Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

1 <= n <= 2 * 10^4
edges.length == n - 1
0 <= a_i, b_i < n
a_i != b_i
All the pairs (a_i, b_i) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

public List<Integer> findMinHeightTrees(int n, int[][] edges) {
    if(n == 1) return List.of(0);

    Set<Integer>[] graph = new Set[n];
    int[] degree = new int[n];

    for(int i = 0; i < graph.length; ++i){
        graph[i] = new HashSet<>();
    }

    for(int[] e: edges){
        graph[e[1]].add(e[0]);
        graph[e[0]].add(e[1]);
        ++degree[e[0]];
        ++degree[e[1]];
    }

    Queue<Integer> q = new LinkedList<>();
    List<Integer> result = new ArrayList<>();

    for(int i = 0; i < degree.length; ++i){
        if(degree[i] == 1) q.add(i);
    }

    while(!q.isEmpty()){
        int size = q.size();
        result.clear();
        while(size-->0){
            int node = q.poll();
            for(int neighbour: graph[node]){
                graph[neighbour].remove(node);
                if(--degree[neighbour] == 1) q.add(neighbour);
            }
            result.add(node);
        }
    }

    return result;
}

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var findMinHeightTrees = function (n, edges) {
  if (n === 1) return [0];

  const graph = new Array(n).fill(null).map(() => new Set());
  const degree = new Array(n).fill(0);

  for (const [a, b] of edges) {
    graph[a].add(b);
    graph[b].add(a);
    degree[a]++;
    degree[b]++;
  }

  const queue = [];
  const result = [];

  for (let i = 0; i < degree.length; i++) {
    if (degree[i] === 1) {
      queue.push(i);
    }
  }

  while (queue.length > 0) {
    const size = queue.length;
    result.length = 0;
    for (let i = 0; i < size; i++) {
      const node = queue.shift();
      for (const neighbor of graph[node]) {
        graph[neighbor].delete(node);
        if (--degree[neighbor] === 1) {
          queue.push(neighbor);
        }
      }
      result.push(node);
    }
  }

  return result;
};

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n == 1:
            return [0]

        graph = [set() for _ in range(n)]
        degree = [0] * n

        for a, b in edges:
            graph[a].add(b)
            graph[b].add(a)
            degree[a] += 1
            degree[b] += 1

        queue = deque()
        result = []

        for i in range(n):
            if degree[i] == 1:
                queue.append(i)

        while queue:
            size = len(queue)
            result.clear()
            for _ in range(size):
                node = queue.popleft()
                for neighbor in graph[node]:
                    graph[neighbor].remove(node)
                    degree[neighbor] -= 1
                    if degree[neighbor] == 1:
                        queue.append(neighbor)
                result.append(node)

        return result

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1) return {0};

        vector<set<int>> graph(n);
        vector<int> degree(n, 0);

        for (const auto& edge : edges) {
            graph[edge[0]].insert(edge[1]);
            graph[edge[1]].insert(edge[0]);
            degree[edge[0]]++;
            degree[edge[1]]++;
        }

        queue<int> q;
        vector<int> result;

        for (int i = 0; i < degree.size(); i++) {
            if (degree[i] == 1) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            int size = q.size();
            result.clear();
            for (int i = 0; i < size; i++) {
                int node = q.front();
                q.pop();
                for (int neighbor : graph[node]) {
                    graph[neighbor].erase(node);
                    degree[neighbor]--;
                    if (degree[neighbor] == 1) {
                        q.push(neighbor);
                    }
                }
                result.push_back(node);
            }
        }

        return result;
    }
};

Time/Space Complexity:

Time Complexity: O(V) where V is number of vertices
Space Complexity: O(V)

Explanation:

Note that time complexity isn't E+V like we had in Course Schedule since by the problem statement edges.length == n - 1 which means E = V - 1 so the time complexity would be O(V + V - 1) = O(2V - 1) = O(V). For the space complexity we have the same, since we're building the graph. We utilize most of the implementation from the course schedule problems but this time since we have bidirectional graph we use sets for adjacency-list (building the graph) since it enables us to remove the neighbours edges quickly. To form the minimum height trees (MHTs) you could first think of two pointers start and end if we want to have a point which is equally distant from both of the pointer we would choose to be in the middle of start and end forming a ^ shape, where the length of lines pointing down is the same, note that if you would shift it a bit to one of the pointer you would get a skewed ^ shape and the height of it would be larger than the height when we choose the middle point. We can expand this logic in graph structure, but instead of having pointer we have "leaves", so we must find middle points (we can call them centroids) which are the nodes who have the "most equally distributed distance" from the leaf nodes. Note that we can have at max two centroids (two if number of nodes is even, and 1 if number of nodes is odd), since if we would have more than two let's say three they would be equally distance from each other so they would form a triangle (cycle in graph which can't be since by the problem statement there is no cycle in the graph), and if we're missing one edge of the triangle that means the one of three nodes is actually the centroid (since it's other two nodes are now leaves equally distant from it). So, the approach we have is to "eat up the leaves", for the first candidates we have the initial vertices with only one edge connecting them to other vertices, and we first remove those, and we keep on adding their neighbor which could become new leaves if the previous node has been already discarded (--degree[neighbour] == 1). With result we keep track of the latest list of candidates/list, and when we're done with iterating over all vertices, that list will contain the last iteration leaves also called centroids. Finally, we return that list containing our centroids.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​