Sort Items by Groups Respecting Dependencies

Sort Items by Groups Respecting Dependencies: There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.

Return a sorted list of the items such that:

The items that belong to the same group are next to each other in the sorted list.
There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).

Return any solution if there is more than one solution and return an empty list if there is no solution.

Example 1:

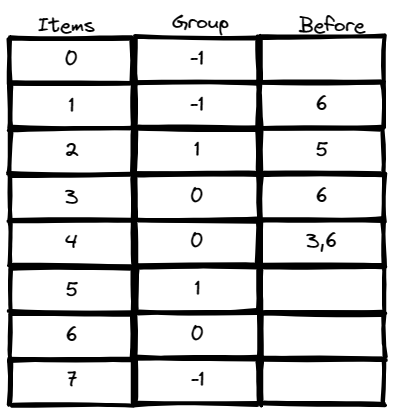
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1],
beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

Example 2:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1],
beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that
4 needs to be before 6 in the sorted list.

Constraints:

1 <= m <= n <= 3 * 10^4
group.length == beforeItems.length == n
-1 <= group[i] <= m - 1
0 <= beforeItems[i].length <= n - 1
0 <= beforeItems[i][j] <= n - 1
i != beforeItems[i][j]
beforeItems[i] does not contain duplicates elements.

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

class Solution {
  Map <Integer, List<Integer>> groupDependencyGraph = new HashMap<>();
  Map <Integer, List<Integer>> itemDependencyGraph = new HashMap<>();

  int[] groupDependencyDegree;
  int[] itemDependencyDegree;

  private void buildGroupsGraph(int[] group, List<List<Integer>> beforeItems, int n) {
    for (int i=0; i < group.length; ++i) {
      int to = group[i];
      List <Integer> items = beforeItems.get(i);
      for (int item : items) {
        int from = group[item];
        if(from != to) {
          if(groupDependencyGraph.get(from) == null){
            groupDependencyGraph.put(from, new ArrayList<>());
          }
          groupDependencyGraph.get(from).add(to);
          ++groupDependencyDegree[to];
        }
      }
    }
  }

  private void buildItemsGraph(List<List<Integer>> beforeItems, int n) {
    for (int i=0; i < n; ++i) {
      List<Integer> items = beforeItems.get(i);
      for (Integer item : items) {
        if(itemDependencyGraph.get(item) == null){
            itemDependencyGraph.put(item, new ArrayList<>());
        }
        itemDependencyGraph.get(item).add(i);
        ++itemDependencyDegree[i];
      }
    }
  }

  private List<Integer> topologicalSort(Map<Integer, List<Integer>> graph, int[] degree, int n) {
    List<Integer> result = new ArrayList<Integer>();
    Queue<Integer> q = new LinkedList();

    for (int key : graph.keySet()) {
      if(degree[key] == 0) {
        q.add(key);
      }
    }

    while(!q.isEmpty()) {
      int node = q.poll();
      result.add(node);
      for (int neighbor : graph.get(node)) {
        if(--degree[neighbor] == 0) {
          q.add(neighbor);
        }
      }
    }
    return result.size() == n ? result : new ArrayList();
  }

  public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
    for (int i=0; i < group.length; ++i) {
      if(group[i] == -1) group[i] = m++;
    }

    IntStream.range(0, m)
    .forEach(i -> groupDependencyGraph.put(i, new ArrayList<>()));

    IntStream.range(0, n)
    .forEach(i -> itemDependencyGraph.put(i, new ArrayList<>()));

    groupDependencyDegree = new int[m];
    itemDependencyDegree = new int[n];

    buildGroupsGraph(group, beforeItems, n);
    buildItemsGraph(beforeItems, n);


    List<Integer> sortedGroups = topologicalSort(groupDependencyGraph, groupDependencyDegree, m);
    List<Integer> sortedItems = topologicalSort(itemDependencyGraph, itemDependencyDegree, n);

    if(sortedGroups.size() == 0 || sortedItems.size() == 0) return new int[0];

    Map<Integer, List<Integer>> groupsToItemsMapping = new HashMap();

    for (Integer item : sortedItems) {
      if(groupsToItemsMapping.get(group[item]) == null){
          groupsToItemsMapping.put(group[item], new ArrayList<>());
      }
      groupsToItemsMapping.get(group[item]).add(item);
    }

    int[] result = new int[n];
    int writer = 0;
    for (Integer g : sortedGroups) {
      List<Integer> items = groupsToItemsMapping.getOrDefault(g, new ArrayList());
      for (Integer item : items) {
        result[writer++] = item;
      }
    }

    return result;
  }
}

/**
 * @param {number} n
 * @param {number} m
 * @param {number[]} group
 * @param {number[][]} beforeItems
 * @return {number[]}
 */

let groupDependencyGraph = new Map();
let itemDependencyGraph = new Map();
let groupDependencyDegree = [];
let itemDependencyDegree = [];

var sortItems = function (n, m, group, beforeItems) {
  for (let i = 0; i < group.length; i++) {
    if (group[i] === -1) group[i] = m++;
  }

  for (let i = 0; i < m; i++) {
    groupDependencyGraph.set(i, []);
  }

  for (let i = 0; i < n; i++) {
    itemDependencyGraph.set(i, []);
  }

  groupDependencyDegree = new Array(m).fill(0);
  itemDependencyDegree = new Array(n).fill(0);

  buildGroupsGraph(group, beforeItems, n);
  buildItemsGraph(beforeItems, n);

  const sortedGroups = topologicalSort(
    groupDependencyGraph,
    groupDependencyDegree,
    m
  );
  const sortedItems = topologicalSort(
    itemDependencyGraph,
    itemDependencyDegree,
    n
  );

  if (sortedGroups.length === 0 || sortedItems.length === 0) return [];

  const groupsToItemsMapping = new Map();

  for (const item of sortedItems) {
    if (!groupsToItemsMapping.has(group[item])) {
      groupsToItemsMapping.set(group[item], []);
    }
    groupsToItemsMapping.get(group[item]).push(item);
  }

  const result = [];
  let writer = 0;
  for (const g of sortedGroups) {
    const items = groupsToItemsMapping.get(g) || [];
    for (const item of items) {
      result[writer++] = item;
    }
  }

  return result;
};

function buildGroupsGraph(group, beforeItems, n) {
  for (let i = 0; i < group.length; i++) {
    const to = group[i];
    const items = beforeItems[i];
    for (const item of items) {
      const from = group[item];
      if (from !== to) {
        if (!groupDependencyGraph.has(from)) {
          groupDependencyGraph.set(from, []);
        }
        groupDependencyGraph.get(from).push(to);
        groupDependencyDegree[to]++;
      }
    }
  }
}

function buildItemsGraph(beforeItems, n) {
  for (let i = 0; i < n; i++) {
    const items = beforeItems[i];
    for (const item of items) {
      if (!itemDependencyGraph.has(item)) {
        itemDependencyGraph.set(item, []);
      }
      itemDependencyGraph.get(item).push(i);
      itemDependencyDegree[i]++;
    }
  }
}

function topologicalSort(graph, degree, n) {
  const result = [];
  const queue = [];

  for (const key of graph.keys()) {
    if (degree[key] === 0) {
      queue.push(key);
    }
  }

  while (queue.length > 0) {
    const node = queue.shift();
    result.push(node);
    for (const neighbor of graph.get(node)) {
      if (--degree[neighbor] === 0) {
        queue.push(neighbor);
      }
    }
  }

  return result.length === n ? result : [];
}

class Solution:
    def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:
        for item in range(n):
            if group[item]==-1:
                group[item]=m
                m+=1

        visited=set()

        indegree_items=[0]*n
        outdegree_items=defaultdict(set)

        indegree_groups=[0]*m
        outdegree_groups=defaultdict(set)

        for i,b in enumerate(beforeItems):
            for before in b:
                if group[before]==group[i]:
                    indegree_items[i]+=1
                    outdegree_items[before].add(i)
                else:
                    if (group[i],group[before]) in visited: continue
                    visited.add((group[i],group[before]))

                    indegree_groups[group[i]]+=1
                    outdegree_groups[group[before]].add(group[i])

        groups=[[] for _ in range(m)]
        for i in range(n):
            groups[group[i]].append(i)

        for gnum,grp in enumerate(groups):
            q=deque()
            for item in grp:
                if indegree_items[item]==0:
                    q.append(item)

            cursorted=[]
            while q:
                current=q.popleft()
                cursorted.append(current)

                for outgoin in outdegree_items[current]:
                    indegree_items[outgoin]-=1

                    if indegree_items[outgoin]==0:
                        q.append(outgoin)
            if len(cursorted)!=len(grp):
                return []
            groups[gnum]=cursorted

        q=deque()
        for grp,num in enumerate(indegree_groups):
            if num==0:
                q.append(grp)
        res=[]
        while q:
            curgroup=q.popleft()

            for item in groups[curgroup]:
                res.append(item)

            for outgoin in outdegree_groups[curgroup]:
                indegree_groups[outgoin]-=1
                if indegree_groups[outgoin]==0:
                    q.append(outgoin)

        if len(res) != n:
            return []

        return res

class Solution {
public:
    vector<int> sortItems(int n, int m, vector<int>& group, vector<vector<int>>& beforeItems) {
        for(int node = 0; node < n; node++)
            if(group[node] == -1)
                group[node] = m++;

        vector<unordered_set<int> > group_graph(m), node_graph(n);
        vector<int> group_indegree(m, 0), node_indegree(n, 0);

        for(auto node = 0; node < n; node++) {
            int dst_group = group[node];
            for(auto src_node: beforeItems[node]) {
                int src_group = group[src_node];
                if(dst_group != src_group && !group_graph[src_group].count(dst_group)) {
                    group_graph[src_group].emplace(dst_group);
                    ++group_indegree[dst_group];
                }

                if(!node_graph[src_node].count(node)) {
                    node_graph[src_node].emplace(node);
                    ++node_indegree[node];
                }
            }
        }

        vector<int> ordered_nodes = topologicalSort(node_graph, node_indegree);
        vector<int> ordered_groups = topologicalSort(group_graph, group_indegree);
        vector<int> order;

        vector<vector<int> > group_ordered_nodes(m);
        for(auto node: ordered_nodes)
            group_ordered_nodes[group[node]].emplace_back(node);

        for(auto group: ordered_groups)
            for(auto node: group_ordered_nodes[group])
                order.emplace_back(node);

        return order;
    }

private:
    vector<int> topologicalSort(vector<unordered_set<int> >& graph, vector<int>& indegree) {
        vector<int> order;
        int processed = 0, n = graph.size();

        queue<int> q;
        for(int node = 0; node < n; node++)
            if(indegree[node] == 0)
                q.emplace(node);

        while(!q.empty()) {
            auto node = q.front();
            q.pop();

            ++processed;
            order.emplace_back(node);
            for(auto neighbor: graph[node]) {
                --indegree[neighbor];
                if(indegree[neighbor] == 0)
                    q.emplace(neighbor);
            }
        }

        return processed < n ? vector<int>{} : order;
    }
};

Time/Space Complexity:

Time Complexity: O((E1+V1) + (E2+V2)) where E1 and V1 are edges and vertices of groups dependency graph, while E2 and V2 are edges and vertices of items dependency graph
Space Complexity: O((E1+V1) + (E2+V2))

Explanation:

If we can create a dependency graph between groups and items we can utilize the two-level topological sort, by sorting first the groups and then the items. If we can get a valid topological sort of both that means, there is no cycle in either of graphs. We build the graphs (adjacency list approach) using the beforeItems information and we also track degree for each node in group and items dependency graphs which are later used in topological sort which we reuse from the solution Course Schedule II. If there is a valid topological order, we build the map that does the mapping from group to items and we build the end result by traversing the sorted order of groups each time taking all the items (in sorted topological order) from each of the groups. The time and space complexity reflect both building the graphs and their respective topological sort.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​