Linked List Cycle II

---

Linked List Cycle II: Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

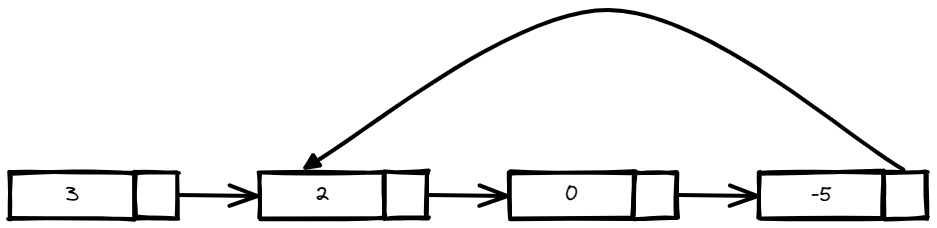
Input: head = [3,2,0,-5], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

---

Example 2:

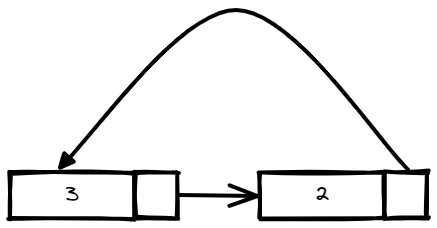
Input: head = [3,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

---

Example 3:

Input: head = [3], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

---

Constraints:

• The number of the nodes in the list is in the range [0, 10^4].
• -10^5 <= Node.val <= 10^5
• pos is -1 or a valid index in the linked-list.

---

Try this Problem on your own or check similar problems:

1. Happy Number
2. Find the Duplicate Number

Solution:

Java

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
  public ListNode detectCycle(ListNode head) {
      if(head == null) return null;

      ListNode slow = head, fast = head;
      boolean cycleDetected = false;

      while(fast != null && fast.next != null){
          slow = slow.next;
          fast = fast.next.next;
          if(slow == fast){
              cycleDetected = true;
              break;
          }
      }
      if(!cycleDetected) return null;

      slow = head;
      while(slow != fast){
          slow = slow.next;
          fast = fast.next;
      }

      return slow;

  }
}

JavaScript

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function (head) {
  if (head === null) return null;

  let slow = head;
  let fast = head;
  let cycleDetected = false;

  while (fast !== null && fast.next !== null) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) {
      cycleDetected = true;
      break;
    }
  }
  if (!cycleDetected) return null;

  slow = head;
  while (slow !== fast) {
    slow = slow.next;
    fast = fast.next;
  }

  return slow;
};

Python

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if head is None:
            return None

        slow = head
        fast = head
        cycleDetected = False

        while fast is not None and fast.next is not None:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                cycleDetected = True
                break
        if not cycleDetected:
            return None

        slow = head
        while slow != fast:
            slow = slow.next
            fast = fast.next

        return slow

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr) return nullptr;

        ListNode* slow = head;
        ListNode* fast = head;
        bool cycleDetected = false;

        while (fast != nullptr && fast->next != nullptr) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) {
                cycleDetected = true;
                break;
            }
        }
        if (!cycleDetected) return nullptr;

        slow = head;
        while (slow != fast) {
            slow = slow->next;
            fast = fast->next;
        }

        return slow;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(1)

---

Explanation:

The solution is a combination of the two implementations Find the Duplicate Number where have detailed explanation on how to find the entry point to cycle if one exists, and Linked List Cycle where we actually detect if a cycle exists. It all comes down to slow and fast pointers and "on your left" approach we already discussed.