Merge Two Sorted Lists

---

Merge Two Sorted Lists: You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists in a one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

Example 1:

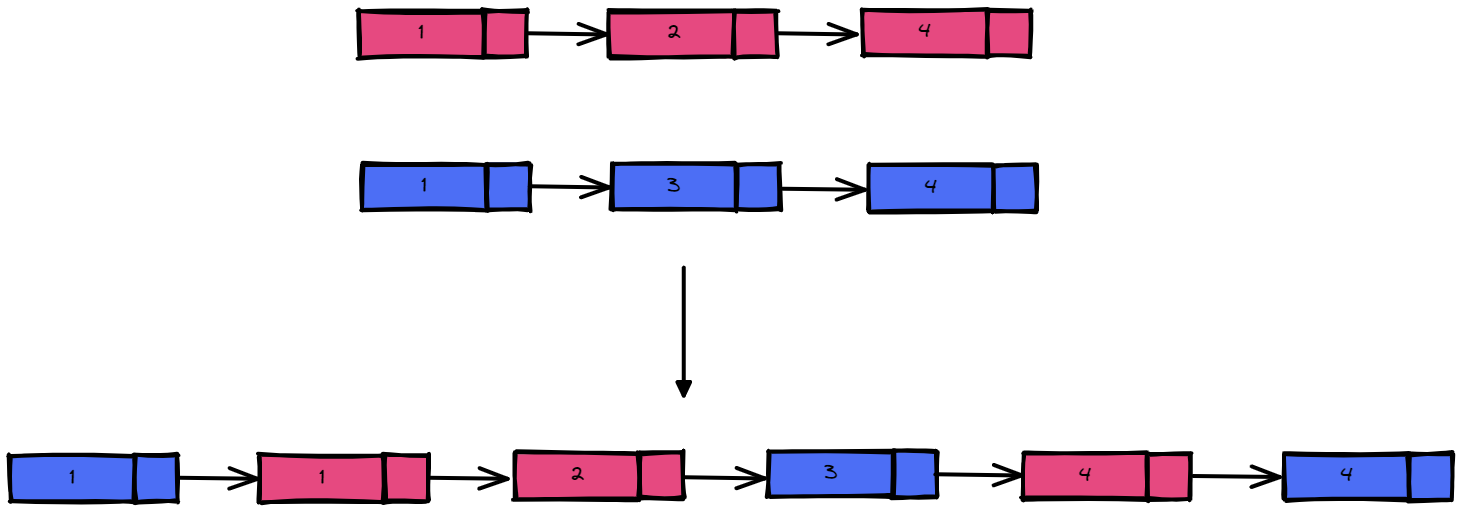
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

---

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

---

Constraints:

• The number of nodes in both lists is in the range [0, 50].
• -100 <= Node.val <= 100
• Both list1 and list2 are sorted in non-decreasing order.

---

Try this Problem on your own or check similar problems:

1. Sort List
2. Merge k Sorted Lists

Solution:

Java

public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
    if(list1 == null || list2 == null) return list1 == null ? list2 : list1;

    ListNode dummy = new ListNode(-1, null), curr = dummy;

    while(list1 != null && list2 != null){
        if(list1.val < list2.val){
            curr.next = list1;
            list1 = list1.next;
        }
        else{
            curr.next = list2;
            list2 = list2.next;
        }

        curr = curr.next;
    }

    if(list1 != null || list2 != null){
        curr.next = list1 != null ? list1 : list2;
    }

    return dummy.next;
}

JavaScript

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 * @return {ListNode}
 */
var mergeTwoLists = function (list1, list2) {
  if (list1 === null || list2 === null) {
    return list1 === null ? list2 : list1;
  }

  let dummy = new ListNode(-1);
  let curr = dummy;

  while (list1 !== null && list2 !== null) {
    if (list1.val < list2.val) {
      curr.next = list1;
      list1 = list1.next;
    } else {
      curr.next = list2;
      list2 = list2.next;
    }

    curr = curr.next;
  }

  if (list1 !== null || list2 !== null) {
    curr.next = list1 !== null ? list1 : list2;
  }

  return dummy.next;
};

Python

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        if list1 is None or list2 is None:
            return list2 if list1 is None else list1

        dummy = ListNode(-1)
        curr = dummy

        while list1 is not None and list2 is not None:
            if list1.val < list2.val:
                curr.next = list1
                list1 = list1.next
            else:
                curr.next = list2
                list2 = list2.next

            curr = curr.next

        if list1 is not None or list2 is not None:
            curr.next = list1 if list1 is not None else list2

        return dummy.next

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if (list1 == nullptr || list2 == nullptr) {
            return list1 == nullptr ? list2 : list1;
        }

        ListNode* dummy = new ListNode(-1);
        ListNode* curr = dummy;

        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val < list2->val) {
                curr->next = list1;
                list1 = list1->next;
            } else {
                curr->next = list2;
                list2 = list2->next;
            }

            curr = curr->next;
        }

        if (list1 != nullptr || list2 != nullptr) {
            curr->next = list1 != nullptr ? list1 : list2;
        }

        return dummy->next;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(min(m,n))
• Space Complexity: O(1)

---

Explanation:

We first check if any of the lists are empty and return the other list (which also can be empty resulting in a final empty list). As always, we utilize the dummy node and define our curr node. We iterate over both lists until one (or both) ends. Each iteration we connect the curr node with the node from list with smaller value and we also move that list iterator (since we already used the current element iterator is pointing to). At the end of loop one of the lists might still have elements to go over and since it's already sorted (input lists are sorted) we can just append it to the result linked list. As always we return dummy.next which points to the head of the resulting linked list. Note that time complexity depends on the numbers of nodes of the smaller of the lists (m and n).