Skip to main content

Find the Duplicate Number

Find the Duplicate Number: Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.

There is only one repeated number in nums, return this repeated number.

You must solve the problem without modifying the array nums and uses only constant extra space.

Example 1:​
Input: nums = [1,3,4,2,2]
Output: 2
Example 2:​
Input: nums = [3,1,3,4,2]
Output: 3
Constraints:​
  • 1 <= n <= 10^5
  • nums.length == n + 1
  • 1 <= nums[i] <= n
  • All the integers in nums appear only once except for precisely one integer which appears two or more times.

Try this Problem on your own or check similar problems:

  1. Set Mismatch
  2. Linked List Cycle
  3. First Missing Positive
Solution:​
public int findDuplicate(int[] nums) {
    int slow = nums[0], fast = nums[nums[0]];

    while(slow != fast){
        slow = nums[slow];
        fast = nums[nums[fast]];
    }

    slow = 0;
    while(slow != fast){
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
}
Time/Space Complexity:​
  • Time Complexity: O(n)
  • Space Complexity: O(1)
Explanation:​

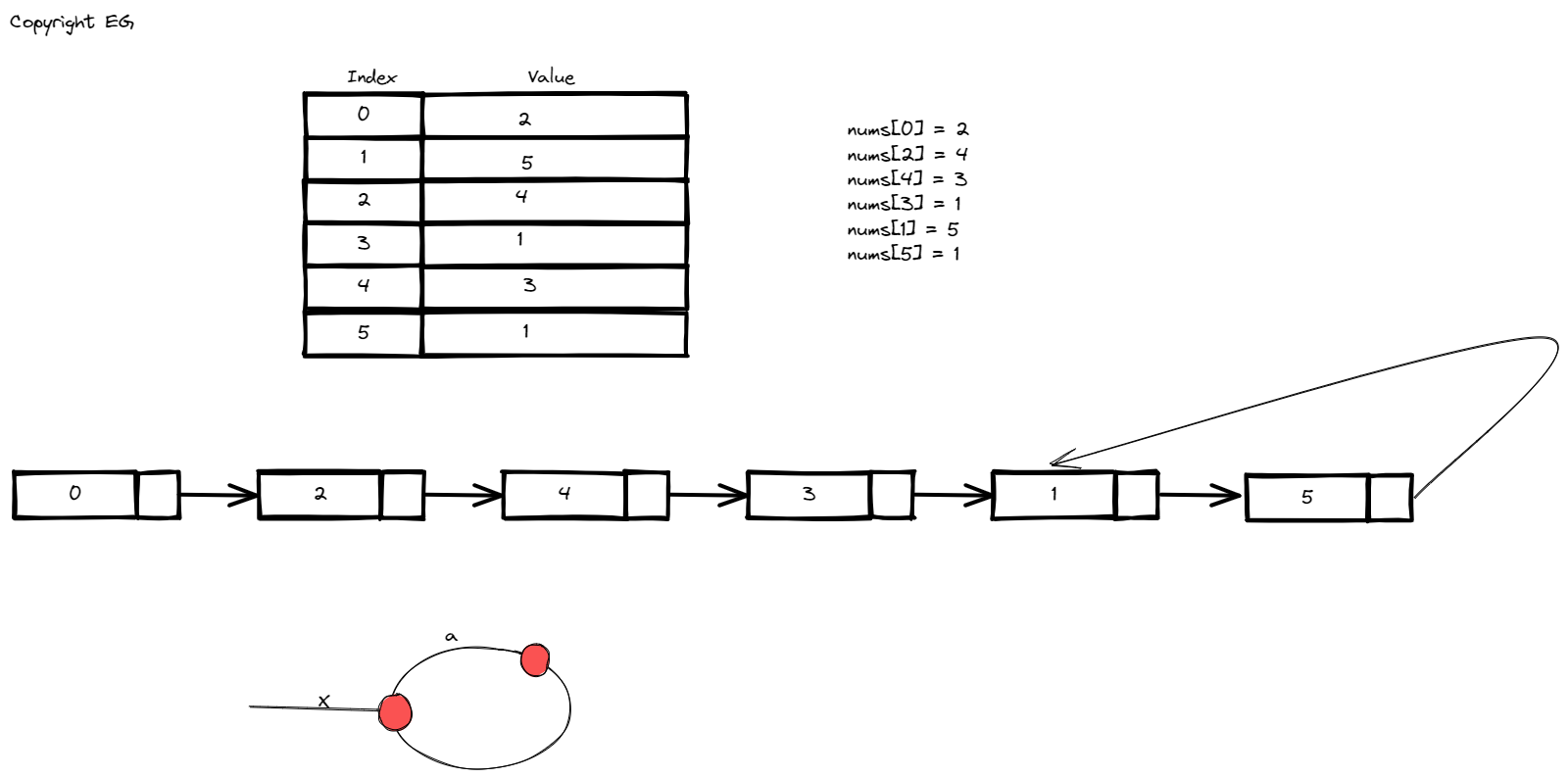
There are a lot of restrictions given by the problem statement, but we can use those restrictions to model our solution. First of all we know we can only use constant space, so any helper data structure is out of question here. We can't modify the input array, so the tricks with making the values at certain index negative and then checking for negative numbers won't work. Can we sort the array? Yes, if sort the array we will arrive at constant space complexity, but O(nlogn) time complexity by checking if the previous element in sorted array is equal to the current (making it the duplicate number). So the question is can we optimize this further? It might come as a surprise that the problem can be reframed to finding the entry point of a cycle just like in linked list (Linked List Cycle). The algorithm is also called "tortoise and hare" or Floyd algorithm. But how do we model the node links just like we have it in linked list with the next pointer?

Note that indices of array are in 0..n (inclusive) range while the values of array are in 1..n inclusive range, so we can be sure that any value of array will point to in-boundary index of array. What would happen if we had 0 as one of the values in array? Well if 0 is the first element we would get a cycle in 0, because it would point to itself (nums[0] = 0), but because of the problem restrictions we know that's not going to happen. So we can model the next relation as next of currentPointer is nums[currentPointer]. How do we detect the cycle? You can check Linked List Cycle, but we have a slow and fast pointer where the fast is moving twice the speed ("on your left joke"). Eventually if there is a cycle the pointers will meet (by the problem statement there is a cycle because there is a duplicate value which is mapped to more than one index).

How do we find the entry point in the cycle (also our duplicate value)? Let's say the distance of slow pointer is defined as d(slow), while the distance of fast pointer is d(fast). By our configuration we know that fast is twice faster than the slow pointer:

d(fast) = 2 * d(slow)

Let's also mark the distance between the starting point (head of the list) and the entry point as X, and distance between meeting point and entry point as a:

d(slow) = X + a
d(fast) = X + nC + a
2 * (X + a) = X + nC + a => X + a = nC

nC is the number of times fast pointer has gone through the cycle where C is the length of the cycle. So we have X + a = nC which means that if we move a fast pointer X steps it should complete one cycle and be at the entry point of cycle again. But what is X? X is distance from starting point (head of the list) and cycle entry point. So if we move slow pointer from the start X steps, and fast pointer from the meeting point X steps they will meet at the entry point of the cycle. We do this in the second loop, by moving the slow pointer again to the start of the list and then moving both slow and fast pointers step by step until they meet. When they meet we found our entry point and also the duplicate and solution for our problem.

image