Spiral Matrix

---

Spiral Matrix: Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

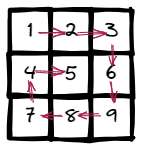
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

---

Example 2:

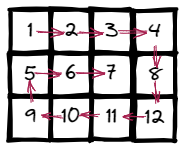
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

---

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

---

Try this Problem on your own or check similar problems:

1. Spiral Matrix II
2. Spiral Matrix III
3. Spiral Matrix IV

Solution:

Java

public List<Integer> spiralOrder(int[][] matrix) {
    int[][] directions  = new int[][] { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1}};
    List<Integer> result = new ArrayList<Integer>();
    int i = 0, m = matrix.length, n = matrix[0].length;
    int x = -1, y = 0, d = 0;

    while(i < m * n){
        int nextX = x + directions[d][0];
        int nextY = y + directions[d][1];
        if(nextX == n || nextX < 0 || nextY == m || nextY < 0 || matrix[nextY][nextX] == -1000){
            d = (d + 1) % directions.length;
            continue;
        }

        result.add(matrix[nextY][nextX]);
        matrix[nextY][nextX] = -1000;

        x = nextX;
        y = nextY;
        ++i;
    }

    return result;
}

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
  const directions = [
    [1, 0],
    [0, 1],
    [-1, 0],
    [0, -1],
  ];
  const result = [];
  let i = 0;
  const m = matrix.length;
  const n = matrix[0].length;
  let x = -1;
  let y = 0;
  let d = 0;

  while (i < m * n) {
    const nextX = x + directions[d][0];
    const nextY = y + directions[d][1];
    if (
      nextX === n ||
      nextX < 0 ||
      nextY === m ||
      nextY < 0 ||
      matrix[nextY][nextX] === -1000
    ) {
      d = (d + 1) % directions.length;
      continue;
    }

    result.push(matrix[nextY][nextX]);
    matrix[nextY][nextX] = -1000;

    x = nextX;
    y = nextY;
    i++;
  }

  return result;
};

Python

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        directions = [[1, 0], [0, 1], [-1, 0], [0, -1]]
        result = []
        i = 0
        m = len(matrix)
        n = len(matrix[0])
        x = -1
        y = 0
        d = 0

        while i < m * n:
            nextX = x + directions[d][0]
            nextY = y + directions[d][1]
            if (
                nextX == n
                or nextX < 0
                or nextY == m
                or nextY < 0
                or matrix[nextY][nextX] == -1000
            ):
                d = (d + 1) % len(directions)
                continue

            result.append(matrix[nextY][nextX])
            matrix[nextY][nextX] = -1000

            x = nextX
            y = nextY
            i += 1

        return result

C++

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<vector<int>> directions = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
        vector<int> result;
        int i = 0;
        int m = matrix.size();
        int n = matrix[0].size();
        int x = -1;
        int y = 0;
        int d = 0;

        while (i < m * n) {
            int nextX = x + directions[d][0];
            int nextY = y + directions[d][1];
            if (nextX == n || nextX < 0 || nextY == m || nextY < 0 || matrix[nextY][nextX] == -1000) {
                d = (d + 1) % directions.size();
                continue;
            }

            result.push_back(matrix[nextY][nextX]);
            matrix[nextY][nextX] = -1000;

            x = nextX;
            y = nextY;
            i++;
        }

        return result;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n*m)
• Space Complexity: O(1)

---

Explanation:

First note that we're using the problem restrictions to define a special marker for already visited elements. In this case it is just a number greater than 100, but if your interviewer doesn’t give you those kinds of restrictions than we can use different approach. One would be to iterate over matrix elements and find the maximum elements and then each visited element will be set to maxElement+1. Pf course there are some limitations because what if we have Integer.MAX_VALUE, in that case we could have some structure to keep track on visited elements (boolean matrix where each element at index visited[i][j] answers the question if the element in input matrix has already been visited). So that's the first part, next how do we create the final output?

Well, we do exactly what the problem asks us, we spirally traverse the matrix. To do that we define direction matrix (or array of tuples) where each element is a direction in which we can move through the matrix (right, down, left, up). We also define the initial coordinates x and y (in this case x=-1 think of it as traversal not started yet). And we iterate over the matrix until we have looped over all elements i == m*n, each time we calculate the new coordinates and check if they are still in the boundary and if the element they are pointing to hasn't been already visited. If they're in boundary and on unvisited element we add that element to a result list and set the coordinates to the new coordinates (the starting point for the next loop iteration).