Longest Consecutive Sequence

Longest Consecutive Sequence: Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.

You must write an algorithm that runs in O(n) time.

Example 1:

Input: nums = [100,4,200,1,3,2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4].
Therefore its length is 4.

Example 2:

Input: nums = [0,3,7,2,5,8,4,6,0,1]
Output: 9

Constraints:

0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

public int longestConsecutive(int[] nums) {
    HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
    int maxSequenceLength = 0;

    for(int i = 0; i < nums.length; ++i){
        if(map.containsKey(nums[i])) continue;
        int left = map.getOrDefault(nums[i] - 1, 0), right = map.getOrDefault(nums[i] + 1, 0);
        int length = left + right + 1;

        if(left > 0){
            map.put(nums[i]-left, length);
        }
        if(right > 0){
            map.put(nums[i]+right, length);
        }
        map.put(nums[i], length);
        maxSequenceLength = Math.max(maxSequenceLength, length);
    }

    return maxSequenceLength;
}

/**
 * @param {number[]} nums
 * @return {number}
 */
var longestConsecutive = function (nums) {
  const map = new Map();
  let maxSequenceLength = 0;

  for (let i = 0; i < nums.length; ++i) {
    if (map.has(nums[i])) continue;
    const left = map.get(nums[i] - 1) || 0;
    const right = map.get(nums[i] + 1) || 0;
    const length = left + right + 1;

    if (left > 0) {
      map.set(nums[i] - left, length);
    }
    if (right > 0) {
      map.set(nums[i] + right, length);
    }
    map.set(nums[i], length);
    maxSequenceLength = Math.max(maxSequenceLength, length);
  }

  return maxSequenceLength;
};

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        map = {}
        maxSequenceLength = 0

        for i in range(len(nums)):
            if nums[i] in map:
                continue
            left = map.get(nums[i] - 1, 0)
            right = map.get(nums[i] + 1, 0)
            length = left + right + 1

            if left > 0:
                map[nums[i] - left] = length
            if right > 0:
                map[nums[i] + right] = length
            map[nums[i]] = length
            maxSequenceLength = max(maxSequenceLength, length)

        return maxSequenceLength

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_map<int, int> map;
        int maxSequenceLength = 0;

        for (int i = 0; i < nums.size(); ++i) {
            if (map.find(nums[i]) != map.end()) {
                continue;
            }
            int left = map.find(nums[i] - 1) != map.end() ? map[nums[i] - 1] : 0;
            int right = map.find(nums[i] + 1) != map.end() ? map[nums[i] + 1] : 0;
            int length = left + right + 1;

            if (left > 0) {
                map[nums[i] - left] = length;
            }
            if (right > 0) {
                map[nums[i] + right] = length;
            }
            map[nums[i]] = length;
            maxSequenceLength = max(maxSequenceLength, length);
        }

        return maxSequenceLength;
    }
};

Time/Space Complexity:

Time Complexity: O(n)
Space Complexity: O(n)

Explanation:

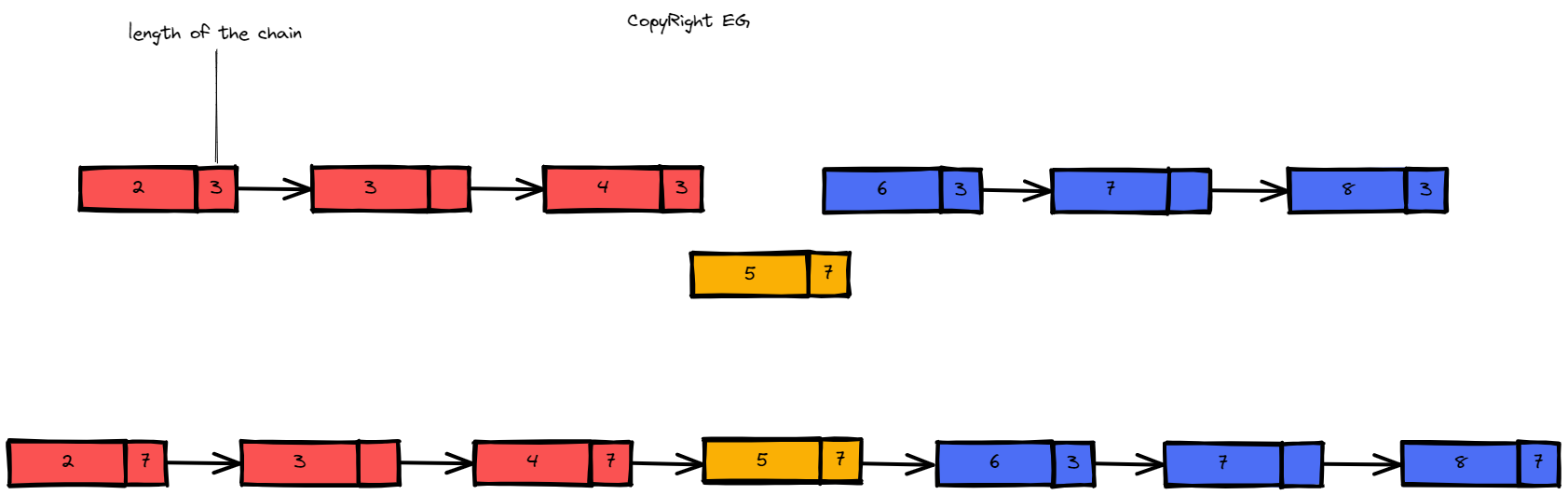
Since we must implement a linear time complexity algorithm the intuitive thing is to think about helper data structures to record subresults while we're iterating over the array. In this case we have a simple hashmap that tracks the length of sequence for each of elements in array. You can think of the sequence as a chain (or linked list) where every element is connected to the next (nums[i]+1) and the previous (nums[i]-1). For each element we check if we have already encountered its previous element in the chain or the next element in the chain. If we have, we set the current length of sequence for previous and next element. Think of each element as a potential link between two long chains, the current element will be the largest element in the left chain and the smallest element in right chain, and it will also connect those two chains (left + right + 1). Then we must update the left and right boundaries of the new sequence (the start and the end of the chain) by marking that total length. The total length is the length of new (combined) chain (e.g. if you have number 5 and you already traversed over 2,3,4 the total length starting at 2 should be 4, the same goes for the right side if you have traversed 6,7,8 and now you're at 5, you should mark the end of the chain 8 with total length of new chain that got connected through number 5). At each iteration we update the maxSequenceLength and we also return it as a result of our function. Also note that we skip duplicated elements so that we don't update the left and right boundaries more than once.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​