Rotate Image

Rotate Image: You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

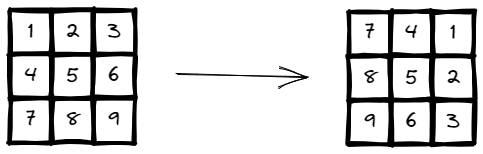
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Constraints:

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

public void rotate(int[][] matrix) {
    int n = matrix.length;

    for(int i = 0; i < n / 2; ++i){
        for(int j = i; j < n - i - 1; ++j){
            int temp = matrix[i][j];
            matrix[i][j] = matrix[n-j-1][i];
            matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
            matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
            matrix[j][n-i-1] = temp;
        }
    }
}

/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var rotate = function (matrix) {
  const n = matrix.length;

  for (let i = 0; i < Math.floor(n / 2); ++i) {
    for (let j = i; j < n - i - 1; ++j) {
      const temp = matrix[i][j];
      matrix[i][j] = matrix[n - j - 1][i];
      matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
      matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
      matrix[j][n - i - 1] = temp;
    }
  }
};

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix)

        for i in range(n // 2):
            for j in range(i, n - i - 1):
                temp = matrix[i][j]
                matrix[i][j] = matrix[n - j - 1][i]
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
                matrix[j][n - i - 1] = temp

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();

        for (int i = 0; i < n / 2; ++i) {
            for (int j = i; j < n - i - 1; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};

Time/Space Complexity:

Time Complexity: O(n^2)
Space Complexity: O(1)

Explanation:

Note that by problem statement we can't use helper data structure since the algorithm has to be in-place (transforms input using no auxiliary data structure). So, we do the iterative transformation over the input matrix. First thing to note is that we're iterating over n/2 submatrices (e.g., for n = 5 we will have the outer wrapper first and last row, first and last column, then we will level down n=3 and do the same). So we set i= 0..n/2-1 inclusive (for loop iterates as long as i < n/2). Next we have j, notice that j is dependent on i since for the first submatrix it can go 0..n-0-1 (n-1 not included) so from the beginning to the second to last element, in the second iteration it can only go from 1..2 (for submatrix 3x3). Now how do we do the actual rotation? Well, we do 4 swaps. First we store the first row elements int temp = matrix[i][j]; since the next operation is destructive to it, and that operation is swapping first row element with first column elements of the submatrix matrix[i][j] = matrix[n-j-1][i];. Then we swap the first column with the last row [n-j-1][i] = matrix[n-i-1][n-j-1]; and the last row with the last column matrix[n-i-1][n-j-1] = matrix[j][n-i-1];. At the end we need to swap the last column with the first row, and we use our temp to do it matrix[j][n-i-1] = temp;. Notice that swapping is done counterclockwise starting from the first column.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​