Largest Rectangle in Histogram

---

Largest Rectangle in Histogram: Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

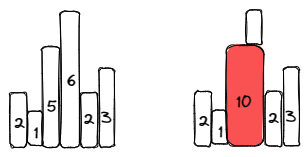
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

---

Example 2:

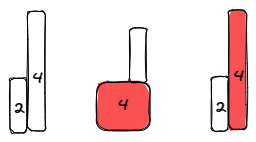
Input: heights = [2,4]
Output: 4

---

Constraints:

• 1 <= heights.length <= 10^5
• 0 <= heights[i] <= 10^4

---

Try this Problem on your own or check similar problems:

1. Maximal Rectangle
2. Maximum Score of a Good Subarray

Solution:

Java

public int largestRectangleArea(int[] heights) {
    int maxArea = 0;
    Deque<Integer> d = new ArrayDeque<>();

    for(int i = 0; i <= heights.length; ++i){
        int height = i == heights.length ? 0 : heights[i];
        while(!d.isEmpty() && heights[d.peekLast()] >= height) {
            int h = heights[d.peekLast()];
            d.pollLast();
            int w = d.isEmpty() ? i : i - d.peekLast() - 1;
            maxArea = Math.max(maxArea, h * w);
        }
        d.addLast(i);
    }

    return maxArea;
}

JavaScript

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function (heights) {
  let maxArea = 0;
  const d = [];

  for (let i = 0; i <= heights.length; i++) {
    const height = i === heights.length ? 0 : heights[i];
    while (d.length && heights[d[d.length - 1]] >= height) {
      const h = heights[d[d.length - 1]];
      d.pop();
      const w = d.length === 0 ? i : i - d[d.length - 1] - 1;
      maxArea = Math.max(maxArea, h * w);
    }
    d.push(i);
  }

  return maxArea;
};

Python

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        maxArea = 0
        d = deque()

        for i in range(len(heights) + 1):
            height = heights[i] if i < len(heights) else 0
            while d and heights[d[-1]] >= height:
                h = heights[d[-1]]
                d.pop()
                w = i if not d else i - d[-1] - 1
                maxArea = max(maxArea, h * w)
            d.append(i)

        return maxArea

C++

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int maxArea = 0;
        deque<int> d;

        for (int i = 0; i <= heights.size(); i++) {
            int height = (i == heights.size()) ? 0 : heights[i];
            while (!d.empty() && heights[d.back()] >= height) {
                int h = heights[d.back()];
                d.pop_back();
                int w = d.empty() ? i : i - d.back() - 1;
                maxArea = max(maxArea, h * w);
            }
            d.push_back(i);
        }

        return maxArea;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We use the monotonic increasing queue here. We know once we encounter a height that's smaller than the element at end of the queue, the maximum area that deque tail element can form is made from elements already in the queue, since it can't cross the current smaller height. So, for each height before we insert it into the queue, we discard any height that's larger than it, while also forming the maxArea with the discarded heights. How do we determine the width of the discarded height? Well, we know the right boundary is current height (index i), since the queue is monotonically increasing, we know that the previous element is the left boundary (we offset their difference by 1 so that we don't count the current height as part of the area). If there is no elements in the stack we know that the discarded height is the smallest added height so far, so it might have discarded other larger heights and the width is just the right boundary i. When we add the last height to the queue, we would end the loop if we traverse over until i < heights.length. To repeat the loop process for the last height we add one additional iteration by faking the n + 1 height (where n is the length of input array heights) to be 0, we know the calculation will be triggered since the queue is in increasing order and heights[d.peekLast()] >= height will be true. We used monotonic queues in problem Daily Temperatures too. The time and space complexity are proportional to the size of the input array heights.