Binary Tree Level Order Traversal

---

Binary Tree Level Order Traversal: Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

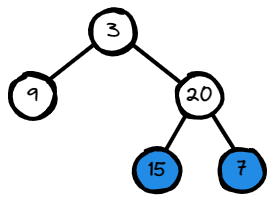
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

---

Example 2:

Input: root = [1]
Output: [[1]]

---

Example 3:

Input: root = []
Output: []

---

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -1000 <= Node.val <= 1000

---

Try this Problem on your own or check similar problems:

1. Binary Tree Level Order Traversal II
2. Average of Levels in Binary Tree
3. Binary Tree Zigzag Level Order Traversal

Solution:

Java

public List<List<Integer>> levelOrder(TreeNode root) {
    if(root == null) return List.of();

    List<List<Integer>> result = new ArrayList<>();
    Queue<TreeNode> q = new LinkedList<>();

    q.add(root);
    while(!q.isEmpty()){
        int size = q.size();
        List<Integer> level = new ArrayList<>();
        while(size-->0){
            TreeNode node = q.poll();
            if(node.left != null){
                q.add(node.left);
            }
            if(node.right != null){
                q.add(node.right);
            }
            level.add(node.val);
        }
        result.add(level);
    }

    return result;
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
  if (!root) {
    return [];
  }

  const result = [];
  const q = [];

  q.push(root);
  while (q.length > 0) {
    const size = q.length;
    const level = [];

    for (let i = 0; i < size; i++) {
      const node = q.shift();

      if (node.left) {
        q.push(node.left);
      }
      if (node.right) {
        q.push(node.right);
      }

      level.push(node.val);
    }

    result.push(level);
  }

  return result;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []

        result = []
        q = deque()

        q.append(root)
        while q:
            size = len(q)
            level = []

            for _ in range(size):
                node = q.popleft()

                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)

                level.append(node.val)

            result.append(level)

        return result

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if (!root) {
            return {};
        }

        std::vector<std::vector<int>> result;
        std::queue<TreeNode*> q;

        q.push(root);
        while (!q.empty()) {
            int size = q.size();
            std::vector<int> level;

            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();

                if (node->left) {
                    q.push(node->left);
                }
                if (node->right) {
                    q.push(node->right);
                }

                level.push_back(node->val);
            }

            result.push_back(level);
        }

        return result;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

The implementation is identical to the Binary Tree Level Order Traversal II and Average of Levels in Binary Tree. We maintain a queue of elements which represent our current level, we loop over current element candidates and try to add left and right nodes if they exist. Finally, we return the list of levels as our result.