Populating Next Right Pointers in Each Node

Populating Next Right Pointers in Each Node: You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node left;
  Node right;
  Node next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL. Initially, all next pointers are set to NULL.

Example 1:

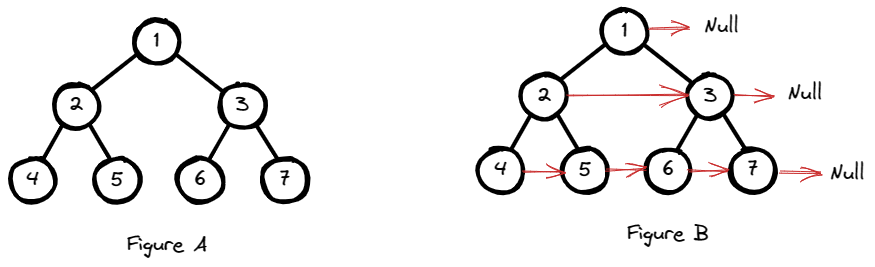
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should
populate each next pointer to point to its next right node,
just like in Figure B. The serialized output is in level order as connected
by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 2^12 - 1].
-1000 <= Node.val <= 1000

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
  public Node connect(Node root) {
    if(root == null) return null;
    Node treeIter = root;

    while(treeIter != null){
        Node levelIter = treeIter;
        while(levelIter != null && levelIter.left != null){
            levelIter.left.next = levelIter.right;
            if(levelIter.next != null){
                levelIter.right.next = levelIter.next.left;
            }
            levelIter = levelIter.next;
        }
        treeIter = treeIter.left;
    }

    return root;
  }
}

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function (root) {
  if (!root) {
    return null;
  }

  let treeIter = root;

  while (treeIter) {
    let levelIter = treeIter;
    while (levelIter && levelIter.left) {
      levelIter.left.next = levelIter.right;
      if (levelIter.next) {
        levelIter.right.next = levelIter.next.left;
      }
      levelIter = levelIter.next;
    }
    treeIter = treeIter.left;
  }

  return root;
};

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if not root:
            return None

        treeIter = root

        while treeIter:
            levelIter = treeIter
            while levelIter and levelIter.left:
                levelIter.left.next = levelIter.right
                if levelIter.next:
                    levelIter.right.next = levelIter.next.left
                levelIter = levelIter.next
            treeIter = treeIter.left

        return root

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        if (!root) {
            return nullptr;
        }

        Node* treeIter = root;

        while (treeIter) {
            Node* levelIter = treeIter;
            while (levelIter && levelIter->left) {
                levelIter->left->next = levelIter->right;
                if (levelIter->next) {
                    levelIter->right->next = levelIter->next->left;
                }
                levelIter = levelIter->next;
            }
            treeIter = treeIter->left;
        }

        return root;
    }
};

Time/Space Complexity:

Time Complexity: O(n)
Space Complexity: O(1)

Explanation:

It's like tree level traversal, so we keep two iterators treeIter which iterates over the tree starting with the root and going to the leaf nodes (so it's always pointing to the current level) and then levelIter which actually traverses through the nodes of the current level treeIter is pointing to. For each level we start by positioning the treeIter to the leftmost node treeIter = treeIter.left;. While we're traversing the level with levelIter we first make the connection between the left and right children of the current level node, and then we check if the current node has a right sibling, if it does we have to make a connection between its right child and its right sibling's left child (levelIter.right.next = levelIter.next.left;). We move the pointer to its right sibling (if there is any), moving to the next node in the current level. Finally, we return the root of the tree as final result. We don't use any additional space so space complexity is O(1), and we iterate over all nodes in the tree which makes the time complexity O(n).

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​