Binary Tree Level Order Traversal II

---

Binary Tree Level Order Traversal II: Given the root of a binary tree, return the bottom-up level order traversal of its nodes' values. (i.e., from left to right, level by level from leaf to root).

Example 1:

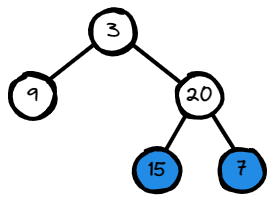
Input: root = [3,9,20,null,null,15,7]
Output: [[15,7],[9,20],[3]]

---

Example 2:

Input: root = [1]
Output: [[1]]

---

Example 3:

Input: root = []
Output: []

---

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -1000 <= Node.val <= 1000

---

Try this Problem on your own or check similar problems:

1. Binary Tree Level Order Traversal
2. Average of Levels in Binary Tree

Solution:

Java

public List<List<Integer>> levelOrderBottom(TreeNode root) {
    if(root == null) return List.of();

    Queue<TreeNode> q = new LinkedList<>();
    List<List<Integer>> result = new ArrayList<>();

    q.add(root);

    while(!q.isEmpty()){
        int size = q.size();
        List<Integer> level = new ArrayList<>();
        while(size-->0){
            TreeNode node = q.poll();
            if(node.left != null){
                q.add(node.left);
            }
            if(node.right != null){
                q.add(node.right);
            }
            level.add(node.val);
        }
        result.add(level);
    }

    Collections.reverse(result);
    return result;
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrderBottom = function (root) {
  if (!root) {
    return [];
  }

  const q = [];
  const result = [];

  q.push(root);

  while (q.length > 0) {
    const size = q.length;
    const level = [];

    for (let i = 0; i < size; i++) {
      const node = q.shift();

      if (node.left) {
        q.push(node.left);
      }
      if (node.right) {
        q.push(node.right);
      }

      level.push(node.val);
    }

    result.push(level);
  }

  result.reverse();
  return result;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []

        q = deque()
        result = []

        q.append(root)

        while q:
            size = len(q)
            level = []

            for _ in range(size):
                node = q.popleft()

                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)

                level.append(node.val)

            result.append(level)

        result.reverse()
        return result

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        if (!root) {
            return {};
        }

        std::queue<TreeNode*> q;
        std::vector<std::vector<int>> result;

        q.push(root);

        while (!q.empty()) {
            int size = q.size();
            std::vector<int> level;

            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();

                if (node->left) {
                    q.push(node->left);
                }
                if (node->right) {
                    q.push(node->right);
                }

                level.push_back(node->val);
            }

            result.push_back(level);
        }

        std::reverse(result.begin(), result.end());
        return result;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We utilize the same approach we did in Average of Levels in Binary Tree by traversing the tree level by level, and at the end we reverse the level traversal so we start from the last level. If you would be asked to do it without reversing the list, you could calculate the maxHeight of tree which would our first list in the final result and then utilize the same approach but this time just writing to the end of array starting from the maxHeight level.