Binary Tree Right Side View
Binary Tree Right Side View:
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:
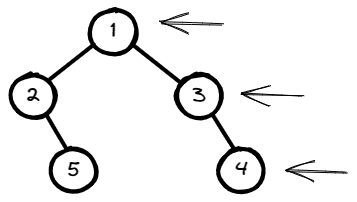
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]
Example 2:
Input: root = [1,null,3]
Output: [1,3]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
class Solution {
public List<Integer> rightSideView(TreeNode root) {
if(root == null) return List.of();
List<Integer> result = new ArrayList<>();
helper(root, 0, result);
return result;
}
private void helper(TreeNode root, int level, List<Integer> result){
if(root == null) return;
if(level == result.size()){
result.add(root.val);
}else{
result.set(level, root.val);
}
helper(root.left, level + 1, result);
helper(root.right, level + 1, result);
}
}
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var rightSideView = function (root) {
if (!root) {
return [];
}
const result = [];
helper(root, 0, result);
return result;
};
function helper(root, level, result) {
if (!root) {
return;
}
if (level === result.length) {
result.push(root.val);
} else {
result[level] = root.val;
}
helper(root.left, level + 1, result);
helper(root.right, level + 1, result);
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
result = []
self.helper(root, 0, result)
return result
def helper(self, root, level, result):
if not root:
return
if level == len(result):
result.append(root.val)
else:
result[level] = root.val
self.helper(root.left, level + 1, result)
self.helper(root.right, level + 1, result)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
if (!root) {
return {};
}
std::vector<int> result;
helper(root, 0, result);
return result;
}
private:
void helper(TreeNode* root, int level, std::vector<int>& result) {
if (!root) {
return;
}
if (level == result.size()) {
result.push_back(root->val);
} else {
result[level] = root->val;
}
helper(root->left, level + 1, result);
helper(root->right, level + 1, result);
}
};
Time/Space Complexity:
- Time Complexity: O(n)
- Space Complexity: O(n)
Explanation:
We can utilize the DFS approach to traverse tree and hold a list which keeps reference to last element in each of tree levels. To keep the track of level we pass level parameter, and we start with the root and 0-level. We can also utilize the BFS tree level traversal we implemented in Binary Tree Level Order Traversal and for each level insert the last node we traverse over (size == 0):
- Java
- JavaScript
- Python
- C++
public List<Integer> rightSideView(TreeNode root) {
if(root == null) return List.of();
Queue<TreeNode> q = new LinkedList<>();
List<Integer> result = new ArrayList<>();
q.add(root);
while(!q.isEmpty()){
int size = q.size();
while(size-->0){
TreeNode node = q.poll();
if(node.left != null){
q.add(node.left);
}
if(node.right != null){
q.add(node.right);
}
if(size == 0){
result.add(node.val);
}
}
}
return result;
}
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var rightSideView = function (root) {
if (root === null) return [];
const queue = [root];
const result = [];
while (queue.length > 0) {
const size = queue.length;
for (let i = 0; i < size; i++) {
const node = queue.shift();
if (node.left !== null) {
queue.push(node.left);
}
if (node.right !== null) {
queue.push(node.right);
}
if (i === size - 1) {
result.push(node.val);
}
}
}
return result;
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
queue = deque([root])
result = []
while queue:
size = len(queue)
for i in range(size):
node = queue.popleft()
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
if i == size - 1:
result.append(node.val)
return result
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
if (root == nullptr)
return {};
std::queue<TreeNode*> q;
std::vector<int> result;
q.push(root);
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
TreeNode* node = q.front();
q.pop();
if (node->left != nullptr) {
q.push(node->left);
}
if (node->right != nullptr) {
q.push(node->right);
}
if (i == size - 1) {
result.push_back(node->val);
}
}
}
return result;
}
};