Maximum Width of Binary Tree
Maximum Width of Binary Tree:
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
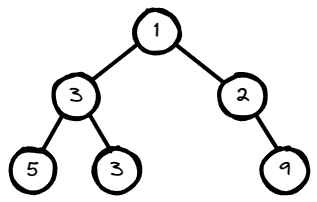
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
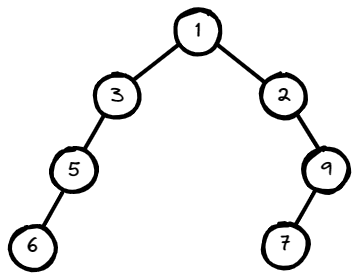
Input: root = [1,3,2,5,null,null,9,6,null,7]
Output: 7
Explanation: The maximum width exists in the fourth
level with length 7 (6,null,null,null,null,null,7).
Example 3:
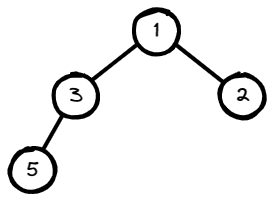
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
public int widthOfBinaryTree(TreeNode root) {
if(root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
Map<TreeNode, Integer> map = new HashMap<>();
int maxWidth = 1;
q.add(root);
map.put(root, 1);
while(!q.isEmpty()){
int size = q.size(), numberOfLevelElements = size;
int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE, offset = map.get(q.peek());
while(numberOfLevelElements-->0){
TreeNode node = q.poll();
int mapping = map.get(node);
min = Math.min(min, mapping - offset);
max = Math.max(max, mapping - offset);
if(node.left != null){
q.add(node.left);
map.put(node.left, 2 * (mapping - offset));
}
if(node.right != null){
q.add(node.right);
map.put(node.right, 2 * (mapping - offset) + 1);
}
}
maxWidth = Math.max(maxWidth, max - min + 1);
}
return maxWidth;
}
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var widthOfBinaryTree = function (root) {
if (root === null) {
return 0;
}
let q = [];
let map = new Map();
let maxWidth = 1;
q.push(root);
map.set(root, 1);
while (q.length > 0) {
let size = q.length,
numberOfLevelElements = size;
let min = Infinity,
max = -Infinity,
offset = map.get(q[0]);
while (numberOfLevelElements-- > 0) {
let node = q.shift();
let mapping = map.get(node);
min = Math.min(min, mapping - offset);
max = Math.max(max, mapping - offset);
if (node.left !== null) {
q.push(node.left);
map.set(node.left, 2 * (mapping - offset));
}
if (node.right !== null) {
q.push(node.right);
map.set(node.right, 2 * (mapping - offset) + 1);
}
}
maxWidth = Math.max(maxWidth, max - min + 1);
}
return maxWidth;
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
q = deque()
mapping = {}
max_width = 1
q.append((root, 1))
mapping[root] = 1
while q:
size = len(q)
min_val, max_val = float('inf'), float('-inf')
for _ in range(size):
node, idx = q.popleft()
min_val = min(min_val, idx)
max_val = max(max_val, idx)
if node.left:
q.append((node.left, 2 * idx))
mapping[node.left] = 2 * idx
if node.right:
q.append((node.right, 2 * idx + 1))
mapping[node.right] = 2 * idx + 1
max_width = max(max_width, max_val - min_val + 1)
return max_width
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
if (root == nullptr)
return 0;
std::queue<TreeNode*> q;
std::unordered_map<TreeNode*, long long> map;
int max_width = 1;
q.push(root);
map[root] = 0; // Start with offset 0
while (!q.empty()) {
int size = q.size();
long long min_val = LLONG_MAX, max_val = LLONG_MIN;
while (size-- > 0) {
TreeNode* node = q.front();
q.pop();
long long idx = map[node];
min_val = std::min(min_val, idx);
max_val = std::max(max_val, idx);
if (node->left) {
q.push(node->left);
map[node->left] = 2 * idx - min_val;
}
if (node->right) {
q.push(node->right);
map[node->right] = 2 * idx + 1 - min_val;
}
}
max_width = std::max(max_width, static_cast<int>(max_val - min_val + 1));
}
return max_width;
}
};
Time/Space Complexity:
- Time Complexity: O(n)
- Space Complexity: O(n)
Explanation:
We utilize the tree level traversal we already implemented in a few solutions including Binary Tree Level Order Traversal. We use an idea that each node in tree if we were to flatten the tree into an array can be represented by an index (e.g. if mark root as 1, we can mark its left node to 2*1=2, and its right node to 2*1+1=3, of course we're assuming 1-index array here, same logic can be applied if we mark root with 0, in that case we would get left node 2n+1=1, and right with 2n+2=2). We use the map for the mapping between a node and its relative index if we were to flatten the tree, and for each level we record the minimum and maximum index and we subtract those to get the maximum width for the current level. Note that we would get to an overflow pretty fast (since we're doubling the mapping each level, Integer.MAX_VALUE = 2^31, so we really need just 32 levels/height of tree to reach the maximum). To solve this, first note that we're not interested in cross-level nodes comparison (comparing node to its parent), we're only interested in relation between the min index node and max index node in the current level, so we can offset their indices to cope with the overflow. To do this we set the first node in level index to 0 and shift other nodes by that offset. Note that we really don't need min = Math.min(min, mapping - offset); since it will always be 0 (index of leftmost node), so in essence we're searching for the rightmost index which is offset by the index of the leftmost one.
The space and time complexity are linear as for every level traversal we iterate over all nodes, and we keep the mapping of all nodes in hashmap which leads us to linear space complexity.