Minimum Depth of Binary Tree

---

Minimum Depth of Binary Tree: Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

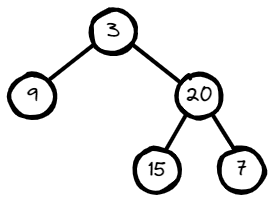
Input: root = [3,9,20,null,null,15,7]
Output: 2

---

Example 2:

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

---

Constraints:

• The number of nodes in the tree is in the range [0, 10^5].
• -1000 <= Node.val <= 1000

---

Try this Problem on your own or check similar problems:

1. Average of Levels in Binary Tree
2. Maximum Depth of Binary Tree
3. Binary Tree Level Order Traversal

Solution:

Java

public int minDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    Queue<TreeNode> q = new LinkedList<>();
    q.add(root);
    int level = 1;

    while(!q.isEmpty()){
        int size = q.size();
        while(size-- > 0) {
            TreeNode node = q.poll();
            if(node.left == null && node.right == null){
                return level;
            }
            if(node.left != null){
                q.add(node.left);
            }
            if(node.right != null){
                q.add(node.right);
            }
        }
        ++level;
    }
    return level;
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function (root) {
  if (!root) {
    return 0;
  }

  const q = [];
  q.push(root);
  let level = 1;

  while (q.length > 0) {
    const size = q.length;

    for (let i = 0; i < size; i++) {
      const node = q.shift();

      if (!node.left && !node.right) {
        return level;
      }

      if (node.left) {
        q.push(node.left);
      }
      if (node.right) {
        q.push(node.right);
      }
    }

    level++;
  }

  return level;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        q = deque()
        q.append(root)
        level = 1

        while q:
            size = len(q)

            for _ in range(size):
                node = q.popleft()

                if not node.left and not node.right:
                    return level

                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)

            level += 1

        return level

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if (!root) {
            return 0;
        }

        std::queue<TreeNode*> q;
        q.push(root);
        int level = 1;

        while (!q.empty()) {
            int size = q.size();

            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();

                if (!node->left && !node->right) {
                    return level;
                }

                if (node->left) {
                    q.push(node->left);
                }
                if (node->right) {
                    q.push(node->right);
                }
            }

            level++;
        }

        return level;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We do a BFS search just like in Average of Levels in Binary Tree, only this time we're keeping track of what level we're currently at and terminate as soon as we find first leaf node (both left and right child is null). Notice that DFS (depth first search) is not the best choice since we're looking for the shortest tree path, in other words imagine a left tree with 10000 nodes contained in the path to the left most tree node, and imagine right leaf node path containing only 1 element. We would spend too much time on the left subtree just to return depth of 2 when we search in right subtree.