All Nodes Distance K in Binary Tree

All Nodes Distance K in Binary Tree: Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

Example 1:

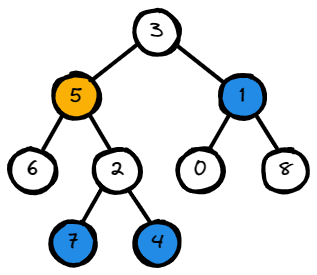
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2
from the target node (with value 5) have values 7, 4, and 1.

Example 2:

Input: root = [1], target = 1, k = 3
Output: []

Constraints:

The number of nodes in the tree is in the range [1, 500].
0 <= Node.val <= 500
All the values Node.val are unique.
target is the value of one of the nodes in the tree.
0 <= k <= 1000

Try this Problem on your own or check similar problems:

Amount of Time for Binary Tree to Be Infected

Solution:

Java
JavaScript
Python
C++

class Solution {
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        List<Integer> result = new ArrayList<>();
        Map<TreeNode, TreeNode> parentMap = new HashMap<>();
        buildParentMap(root, null, parentMap, target);
        TreeNode prev = null;
        while(target != null && k >= 0){
            searchForKDistantNodes(target, prev, k, result);
            prev = target;
            target = parentMap.get(target);
            --k;
        }
        return result;
    }

    private void buildParentMap(TreeNode root, TreeNode prev, Map<TreeNode, TreeNode> parentMap, TreeNode target){
        if(root == null) return;
        if(prev != null){
            parentMap.put(root, prev);
        }
        if(root == target) return;
        buildParentMap(root.left, root, parentMap, target);
        buildParentMap(root.right, root, parentMap, target);
    }

    private void searchForKDistantNodes(TreeNode start, TreeNode prevTarget, int k, List<Integer> result){
        if(start == null || start == prevTarget) return;
        if(k == 0){
            result.add(start.val);
            return;
        }
        searchForKDistantNodes(start.left, prevTarget, k - 1, result);
        searchForKDistantNodes(start.right, prevTarget, k - 1, result);
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} target
 * @param {number} k
 * @return {number[]}
 */
var distanceK = function (root, target, k) {
  const result = [];
  const parentMap = new Map();
  buildParentMap(root, null, parentMap, target);
  let prev = null;
  while (target !== null && k >= 0) {
    searchForKDistantNodes(target, prev, k, result);
    prev = target;
    target = parentMap.get(target);
    --k;
  }
  return result;
};

function buildParentMap(root, prev, parentMap, target) {
  if (root === null) return;
  if (prev !== null) {
    parentMap.set(root, prev);
  }
  if (root === target) return;
  buildParentMap(root.left, root, parentMap, target);
  buildParentMap(root.right, root, parentMap, target);
}

function searchForKDistantNodes(start, prevTarget, k, result) {
  if (start == null || start === prevTarget) return;
  if (k === 0) {
    result.push(start.val);
    return;
  }
  searchForKDistantNodes(start.left, prevTarget, k - 1, result);
  searchForKDistantNodes(start.right, prevTarget, k - 1, result);
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
        result = []
        parentMap = {}
        self.buildParentMap(root, None, parentMap, target)
        prev = None
        while target and k >= 0:
            self.searchForKDistantNodes(target, prev, k, result)
            prev = target
            target = parentMap.get(target)
            k -= 1
        return result

    def buildParentMap(self,root, prev, parentMap, target):
        if not root:
            return
        if prev:
            parentMap[root] = prev
        if root == target:
            return
        self.buildParentMap(root.left, root, parentMap, target)
        self.buildParentMap(root.right, root, parentMap, target)

    def searchForKDistantNodes(self, start, prevTarget, k, result):
        if not start or start == prevTarget:
            return
        if k == 0:
            result.append(start.val)
            return
        self.searchForKDistantNodes(start.left, prevTarget, k - 1, result)
        self.searchForKDistantNodes(start.right, prevTarget, k - 1, result)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
        vector<int> result;
        unordered_map<TreeNode*, TreeNode*> parentMap;
        buildParentMap(root, nullptr, parentMap, target);
        TreeNode* prev = nullptr;
        while (target && k >= 0) {
            searchForKDistantNodes(target, prev, k, result);
            prev = target;
            target = parentMap[target];
            --k;
        }
        return result;
    }

private:
    void buildParentMap(TreeNode* root, TreeNode* prev, unordered_map<TreeNode*, TreeNode*>& parentMap, TreeNode* target) {
        if (!root) return;
        if (prev) {
            parentMap[root] = prev;
        }
        if (root == target) return;
        buildParentMap(root->left, root, parentMap, target);
        buildParentMap(root->right, root, parentMap, target);
    }

    void searchForKDistantNodes(TreeNode* start, TreeNode* prevTarget, int k, vector<int>& result) {
        if (!start || start == prevTarget) return;
        if (k == 0) {
            result.push_back(start->val);
            return;
        }
        searchForKDistantNodes(start->left, prevTarget, k - 1, result);
        searchForKDistantNodes(start->right, prevTarget, k - 1, result);
    }


};

Time/Space Complexity:

Time Complexity: O(n)
Space Complexity: O(n)

Explanation:

We can first ask the interviewer if the target exists in the tree. We can note immediately that finding k distant nodes from the targetNode going down the tree is nothing but a regular search (checking left and right subtree) by keeping track of the distance we traveled in the tree, we use searchForKDistantNodes and if k == 0 we just add the node since its distance is k from the start. The problem is going up in the tree and searching from the parent of the target node, to do that we have to build the parent relation in the tree. We utilize the buildParentMap and traverse to the target while keeping the track of parents. After we have built the parent relation, we can first start from the target and searchForKDistantNodes, then move up to its parent and search again. We repeat this process of going up to the parent as long as the node has parents, and it makes sense to go up (k >= 0). We also keep track of the previous target so that we don't search in each of subtrees multiple times start == prevTarget. Space and time complexity are linear since we traverse at most n nodes and for space since we have the recursion stack and parentMap.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​