Validate Binary Search Tree

---

Validate Binary Search Tree: Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3]
Output: true

---

Example 2:

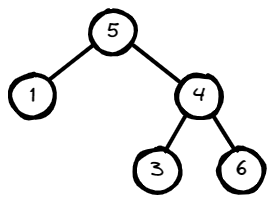
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

---

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• -2^31 <= Node.val <= 2^31 - 1

---

Try this Problem on your own or check similar problems:

1. Binary Tree Inorder Traversal
2. Find Mode in Binary Search Tree

Solution:

Java

class Solution {
  public boolean isValidBST(TreeNode root) {
      return helper(root, null, null);
  }

  private boolean helper(TreeNode root, Integer minimumValue, Integer maximumValue){
      if(root == null) return true;
      if((minimumValue != null && root.val <= minimumValue) || (maximumValue != null && root.val >= maximumValue)) return false;

      return helper(root.left, minimumValue, root.val) && helper(root.right, root.val, maximumValue);
  }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  return helper(root, null, null);
};

function helper(root, minimumValue, maximumValue) {
  if (root === null) return true;
  if (
    (minimumValue !== null && root.val <= minimumValue) ||
    (maximumValue !== null && root.val >= maximumValue)
  )
    return false;

  return (
    helper(root.left, minimumValue, root.val) &&
    helper(root.right, root.val, maximumValue)
  );
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        return self.helper(root, float('-inf'), float('inf'))

    def helper(self, root, minimumValue, maximumValue):
        if root is None:
            return True
        if (minimumValue is not None and root.val <= minimumValue) or (maximumValue is not None and root.val >= maximumValue):
            return False

        return self.helper(root.left, minimumValue, root.val) and self.helper(root.right, root.val, maximumValue)

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return helper(root, nullptr, nullptr);
    }

private:
    bool helper(TreeNode* root, TreeNode* minNode, TreeNode* maxNode) {
        if (root == nullptr)
            return true;

        if (minNode != nullptr && root->val <= minNode->val)
            return false;

        if (maxNode != nullptr && root->val >= maxNode->val)
            return false;

        return helper(root->left, minNode, root) && helper(root->right, root, maxNode);
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

The recursive algorithm is actually explained by the problem statement, we check if the root val is in boundary and then check both left and right subtree passing the right boundaries to helper function (for left subtree, we know the maximum value can be that of the root, while for the right subtree we know that the minimum value must be the root value). We pass null as the initial value for minimumValue and maximumValue since node values can be Integer.MIN_VALUE = -2^31 or Integer.MAX_VALUE = 2^31 - 1, and we do the additional guard check for null value when checking the boundaries. The solution yields a linear space and time complexity (since for space we have a recursions stack for right and left skewed trees).