Maximum Binary Tree

Maximum Binary Tree: You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.

Recursively build the left subtree on the subarray prefix to the left of the maximum value. Recursively build the right subtree on the subarray suffix to the right of the maximum value. Return the maximum binary tree built from nums.

Example 1:

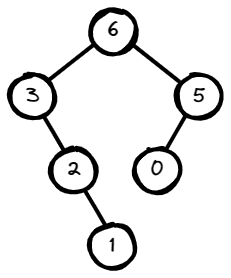
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1]
    and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

Example 2:

Input: nums = [3,2,1]
Output: [3,null,2,null,1]

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
All integers in nums are unique.

Try this Problem on your own or check similar problems:

Maximum Binary Tree II

Solution:

Java
JavaScript
Python
C++

public TreeNode constructMaximumBinaryTree(int[] nums) {
    Deque<TreeNode> d = new ArrayDeque<>();

    for(int num: nums){
        TreeNode node = new TreeNode(num);
        while(d.size() > 0 && d.peekLast().val < num){
            node.left = d.pollLast();
        }
        if(d.size() > 0){
            d.peekLast().right = node;
        }
        d.addLast(node);
    }
    return d.getFirst();
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function (nums) {
  const stack = [];

  for (const num of nums) {
    const node = new TreeNode(num);

    while (stack.length > 0 && stack[stack.length - 1].val < num) {
      node.left = stack.pop();
    }

    if (stack.length > 0) {
      stack[stack.length - 1].right = node;
    }

    stack.push(node);
  }

  return stack[0];
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        stack = []

        for num in nums:
            node = TreeNode(num)

            while len(stack) > 0 and stack[-1].val < num:
                node.left = stack.pop()

            if len(stack) > 0:
                stack[-1].right = node

            stack.append(node)

        return stack[0]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        deque<TreeNode*> d;

        for (int num : nums) {
            TreeNode* node = new TreeNode(num);

            while (!d.empty() && d.back()->val < num) {
                node->left = d.back();
                d.pop_back();
            }

            if (!d.empty()) {
                d.back()->right = node;
            }

            d.push_back(node);
        }

        return d.front();
    }
};

Time/Space Complexity:

Time Complexity: O(n)
Space Complexity: O(n)

Explanation:

A straightforward solution would be to just follow the algorithm described in the problem statement:

Java
JavaScript
Python
C++

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return generateTree(nums, 0, nums.length);
    }

    private TreeNode generateTree(int[] nums, int start, int end){
        if(start == end) return null;

        int maxElementIdx = findMaxIndex(nums, start, end);

        TreeNode root = new TreeNode(nums[maxElementIdx]);
        root.left =  generateTree(nums, start, maxElementIdx);
        root.right = generateTree(nums, maxElementIdx + 1, end);

        return root;
    }

    private int findMaxIndex(int[] nums, int start, int end){
        int maxElement = Integer.MIN_VALUE, idx = -1;
        for(int i = start; i < end; ++i){
            if(nums[i] > maxElement){
                maxElement = nums[i];
                idx = i;
            }
        }
        return idx;
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function (nums) {
  return generateTree(nums, 0, nums.length);
};
var generateTree = function (nums, start, end) {
  if (start === end) return null;

  var maxElementIdx = findMaxIndex(nums, start, end);

  var root = new TreeNode(nums[maxElementIdx]);
  root.left = generateTree(nums, start, maxElementIdx);
  root.right = generateTree(nums, maxElementIdx + 1, end);

  return root;
};

var findMaxIndex = function (nums, start, end) {
  var maxElement = Number.MIN_VALUE,
    idx = -1;
  for (var i = start; i < end; ++i) {
    if (nums[i] > maxElement) {
      maxElement = nums[i];
      idx = i;
    }
  }
  return idx;
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        return self.generateTree(nums, 0, len(nums))

    def generateTree(self, nums: List[int], start: int, end: int) -> TreeNode:
        if start == end:
            return None

        maxElementIdx = self.findMaxIndex(nums, start, end)

        root = TreeNode(nums[maxElementIdx])
        root.left = self.generateTree(nums, start, maxElementIdx)
        root.right = self.generateTree(nums, maxElementIdx + 1, end)

        return root

    def findMaxIndex(self, nums: List[int], start: int, end: int) -> int:
        maxElement = float('-inf')
        idx = -1
        for i in range(start, end):
            if nums[i] > maxElement:
                maxElement = nums[i]
                idx = i
        return idx

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return generateTree(nums, 0, nums.size());
    }

private:
    TreeNode* generateTree(vector<int>& nums, int start, int end) {
        if (start == end) return nullptr;

        int maxElementIdx = findMaxIndex(nums, start, end);

        TreeNode* root = new TreeNode(nums[maxElementIdx]);
        root->left = generateTree(nums, start, maxElementIdx);
        root->right = generateTree(nums, maxElementIdx + 1, end);

        return root;
    }

    int findMaxIndex(vector<int>& nums, int start, int end) {
        int maxElement = INT_MIN;
        int idx = -1;
        for (int i = start; i < end; ++i) {
            if (nums[i] > maxElement) {
                maxElement = nums[i];
                idx = i;
            }
        }
        return idx;
    }
};

We create a helper function generateTree which finds the max element and creates root that will hold that value and recursively build left (start..maxElementIdx in array) and right tree (maxElementIdx+1..end) and just return the root. This solution leads to a quadratic time complexity because of the findMaxIndex function (which is completed in linear time complexity, in case when we have a sorted array) which is called n times (for each node in the tree/element in array).

However we can note that for each node we add to the tree we can form a left subtree for it by checking all added nodes that have a value smaller than it d.peekLast().val < num until we reach a node that has a larger value and since the node's value appeared later in the nums we can add it to the right subtree of the node that has larger value d.peekLast().right = node;. For this we utilize the Deque interface and we finally return the head of the deque (you can think of it as double linked list, we have access to both head and tail).

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​