Binary Tree Maximum Path Sum

---

Binary Tree Maximum Path Sum: A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

---

Example 2:

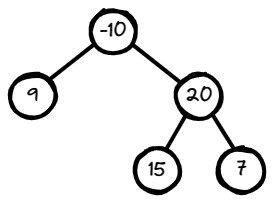
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

---

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 10^4].
• -1000 <= Node.val <= 1000

---

Try this Problem on your own or check similar problems:

1. Path Sum
2. Sum Root to Leaf Numbers
3. Longest Univalue Path

Solution:

Java

class Solution {
  int maxSum = Integer.MIN_VALUE;
  public int maxPathSum(TreeNode root) {
      helper(root);
      return maxSum;
  }
  private int helper(TreeNode root){
      if(root == null) return 0;

      int onlyRootSum = root.val;
      int leftSum = helper(root.left);
      int rightSum = helper(root.right);

      int rootOrOneSubtree = Math.max(onlyRootSum, onlyRootSum + Math.max(leftSum, rightSum));
      int max = Math.max(rootOrOneSubtree, onlyRootSum + leftSum + rightSum);
      if(max > maxSum) maxSum = max;

      return rootOrOneSubtree;
  }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxPathSum = function (root) {
  maxSum = Number.MIN_SAFE_INTEGER;
  helper(root);
  return maxSum;
};

var helper = function (root) {
  if (root === null) return 0;

  var onlyRootSum = root.val;
  var leftSum = helper(root.left);
  var rightSum = helper(root.right);

  var rootOrOneSubtree = Math.max(
    onlyRootSum,
    onlyRootSum + Math.max(leftSum, rightSum)
  );
  var maximum = Math.max(rootOrOneSubtree, onlyRootSum + leftSum + rightSum);
  if (maximum > maxSum) maxSum = maximum;

  return rootOrOneSubtree;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    maxSum = float('-inf')

    def maxPathSum(self, root: Optional[TreeNode]) -> int:
      self.helper(root)
      return self.maxSum

    def helper(self, root):
        if not root:
            return 0

        onlyRootSum = root.val
        leftSum = self.helper(root.left)
        rightSum = self.helper(root.right)

        rootOrOneSubtree = max(onlyRootSum, onlyRootSum + max(leftSum, rightSum))
        maximum = max(rootOrOneSubtree, onlyRootSum + leftSum + rightSum)
        if maximum > self.maxSum:
            self.maxSum = maximum

        return rootOrOneSubtree

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxPathSum(TreeNode* root) {
        helper(root);
        return maxSum;
    }

private:
   int maxSum = INT_MIN;
   int helper(TreeNode* root) {
      if (root == nullptr) return 0;

      int onlyRootSum = root->val;
      int leftSum = helper(root->left);
      int rightSum = helper(root->right);

      int rootOrOneSubtree = max(onlyRootSum, onlyRootSum + max(leftSum, rightSum));
      int maximum = max(rootOrOneSubtree, onlyRootSum + leftSum + rightSum);
      if (maximum > maxSum) maxSum = maximum;

      return rootOrOneSubtree;
  }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We traverse all tree nodes which leads to linear time complexity and space complexity because of the recursion stack (which in skewed tree can reach n calls). We have a global variable maxSum which will be updated deep down in the tree, alternatively we could have created a class only holding a max value and pass it as reference to the helper function. The helper function is the core of the solution and it recursively traverses the tree each time checking if we can update the maxSum. For each node we have 3 choices:

• Pick only the node value as maximum sum
• Pick the sum of the node with its maximum sum subtree
• Or pick the whole subtree rooted in that node

The only question left is what do we return as max value to the previous recursive call? We can't return the value we got by having the subtree rooted in the current node, since that means we can't include the previous recursive call node in the max sum path (because we're rooted now in the current node), so we return the max value from either choosing only the current node or choosing the node and its larger sum subtreee.