Lowest Common Ancestor of a Binary Tree

---

Lowest Common Ancestor of a Binary Tree: Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

“The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

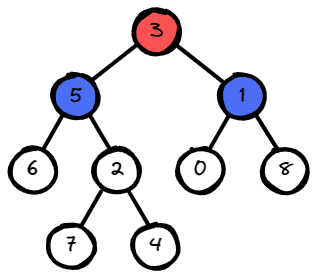
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

---

Example 2:

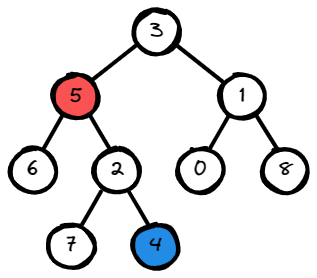
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a
descendant of itself according to the LCA definition.

---

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

---

Constraints:

• The number of nodes in the tree is in the range [2, 10^5].
• -10^9 <= Node.val <= 10^9
• All Node.val are unique.
• p != q
• p and q will exist in the tree.

---

Try this Problem on your own or check similar problems:

1. Step-By-Step Directions From a Binary Tree Node to Another
2. Lowest Common Ancestor of a Binary Tree II

Solution:

Java

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  if(root == null || root == p || root == q) return root;
  TreeNode left = lowestCommonAncestor(root.left, p, q);
  TreeNode right = lowestCommonAncestor(root.right, p, q);
  return left != null && right != null ? root : (left != null ? left : right);
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  if (root === null || root === p || root === q) return root;
  const left = lowestCommonAncestor(root.left, p, q);
  const right = lowestCommonAncestor(root.right, p, q);
  return left !== null && right !== null ? root : left !== null ? left : right;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if root is None or root == p or root == q:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        return root if left is not None and right is not None else (left if left is not None else right)

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr || root == p || root == q)
            return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        return (left != nullptr && right != nullptr) ? root : ((left != nullptr) ? left : right);
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We should first check with the interviewer if can be sure that both p and q exist in the tree, since they do by the problem constraints we can move to the solution. There are three scenarios here:

• The root is equal to either one of p or q so it must be the Lowest Common Ancestor (LCA).
• If not, we check both left and right subtree and if both are non-null, we know that we have p on one side while q on the other side of the root which makes the current root node the LCA.
• Otherwise we have both on either left or right side and we return the side which is not null and eventually the solution pops up to the first recursion call where we return it as our result.

The space and time complexity are linear since at worst case scenario we could iterate over all the nodes in tree and for the space we could have the recursion stack of skewed trees.