Path Sum III

Path Sum III: Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Example 1:

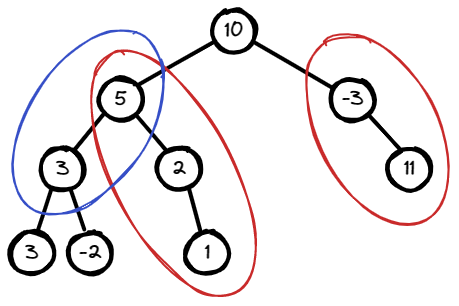
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.

Example 2:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3

Constraints:

The number of nodes in the tree is in the range [0, 1000].
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

class Solution {
  public int pathSum(TreeNode root, int targetSum) {
      Map<Long, Integer> pathSums = new HashMap<>();
      pathSums.put(0L, 1);
      return helper(root, targetSum, 0L, pathSums);
  }

  private int helper(TreeNode root, int targetSum, long currentSum, Map<Long, Integer> pathSums){
      if(root == null) return 0;

      currentSum += root.val;
      int count = pathSums.getOrDefault(currentSum - targetSum, 0);
      pathSums.put(currentSum, pathSums.getOrDefault(currentSum, 0) + 1);

      count += helper(root.left, targetSum, currentSum, pathSums);
      count += helper(root.right, targetSum, currentSum, pathSums);

      pathSums.put(currentSum, pathSums.getOrDefault(currentSum, 0) - 1);
      if(pathSums.get(currentSum) <= 0) pathSums.remove(currentSum);

      return count;
  }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function (root, targetSum) {
  const pathSums = new Map();
  pathSums.set(0, 1);
  return helper(root, targetSum, 0, pathSums);
};

function helper(root, targetSum, currentSum, pathSums) {
  if (root === null) return 0;

  currentSum += root.val;
  let count = pathSums.get(currentSum - targetSum) || 0;
  pathSums.set(currentSum, (pathSums.get(currentSum) || 0) + 1);

  count += helper(root.left, targetSum, currentSum, pathSums);
  count += helper(root.right, targetSum, currentSum, pathSums);

  pathSums.set(currentSum, (pathSums.get(currentSum) || 0) - 1);
  if (pathSums.get(currentSum) <= 0) pathSums.delete(currentSum);

  return count;
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        pathSums = {0: 1}
        return self.helper(root, targetSum, 0, pathSums)

    def helper(self, root, targetSum, currentSum, pathSums):
        if root is None:
            return 0

        currentSum += root.val
        count = pathSums.get(currentSum - targetSum, 0)
        pathSums[currentSum] = pathSums.get(currentSum, 0) + 1

        count += self.helper(root.left, targetSum, currentSum, pathSums)
        count += self.helper(root.right, targetSum, currentSum, pathSums)

        pathSums[currentSum] = pathSums.get(currentSum, 0) - 1
        if pathSums[currentSum] <= 0:
            del pathSums[currentSum]

        return count

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) {
        unordered_map<long, int> pathSums;
        pathSums[0] = 1;
        return helper(root, targetSum, 0, pathSums);
    }

private:
    int helper(TreeNode* root, int targetSum, long currentSum, unordered_map<long, int>& pathSums) {
      if (root == nullptr) return 0;

      currentSum += root->val;
      int count = pathSums[currentSum - targetSum];
      pathSums[currentSum] += 1;

      count += helper(root->left, targetSum, currentSum, pathSums);
      count += helper(root->right, targetSum, currentSum, pathSums);

      pathSums[currentSum] -= 1;
      if (pathSums[currentSum] <= 0) pathSums.erase(currentSum);

      return count;
  }
};

Time/Space Complexity:

Time Complexity: O(n)
Space Complexity: O(n)

Explanation:

Note that this modification to the problem Path Sum II since we can also choose non "root-to-leaf" paths that yield the desired targetSum, but we still reuse the idea of backtracking while traversing through the tree. You can think of the root-to-leaf paths as array and that we're trying to find subarray (nodes along that path) forming the sum targetSum. If you recall we already had a good approach for getting the sum of subarray elements in Range Query Sum Immutable which is based on prefix sum idea. So, we have a map that tracks counts of each of subarray sums we have faced so far, if we add the current node, how do we know there is subarray up until that node which sum is equal to targetSum? Well there is a subarray sum currentSum - targetSum (we can have more of them in the path to the current node, since node values can be negative numbers e.g. one path summing to 10, and then two nodes 5 and -5 summing to 0 on our path to the current node) we can be sure that subarray starting from the sum currentSum - targetSum up to currentSum (added current node value) yields targetSum (remember prefixSum currentSum - (currentSum - targetSum) = targetSum). We check both the left and right subtree of the current node to see if can form more of these subpaths/subarrays. Finally, we backtrack and remove the currentSum from the prefix sum map and return the total count of paths summing to targetSum.

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​