Path Sum II
Path Sum II:
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.
A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.
Example 1:
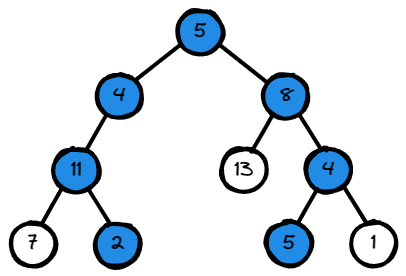
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]
Explanation: There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
Example 2:
Input: root = [1,2,3], targetSum = 5
Output: []
Example 3:
Input: root = [1,2], targetSum = 0
Output: []
Constraints:
The number of nodes in the tree is in the range [0, 5000].-1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
helper(root, targetSum, 0, result, new ArrayList<>());
return result;
}
private void helper(TreeNode root, int targetSum, int currentSum, List<List<Integer>> result, List<Integer> currentRootToLeafNodes){
if(root == null) return;
currentRootToLeafNodes.add(root.val);
if(root.left == null && root.right == null && currentSum + root.val == targetSum){
result.add(new ArrayList<>(currentRootToLeafNodes));
}else{
helper(root.left, targetSum, currentSum + root.val, result, currentRootToLeafNodes);
helper(root.right, targetSum, currentSum + root.val, result, currentRootToLeafNodes);
}
currentRootToLeafNodes.remove(currentRootToLeafNodes.size() - 1);
}
}
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {number[][]}
*/
var pathSum = function (root, targetSum) {
const result = [];
helper(root, targetSum, 0, result, []);
return result;
};
function helper(root, targetSum, currentSum, result, currentRootToLeafNodes) {
if (root === null) return;
currentRootToLeafNodes.push(root.val);
if (
root.left === null &&
root.right === null &&
currentSum + root.val === targetSum
) {
result.push([...currentRootToLeafNodes]);
} else {
helper(
root.left,
targetSum,
currentSum + root.val,
result,
currentRootToLeafNodes
);
helper(
root.right,
targetSum,
currentSum + root.val,
result,
currentRootToLeafNodes
);
}
currentRootToLeafNodes.pop();
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
result = []
self.helper(root, targetSum, 0, result, [])
return result
def helper(self, root, targetSum, currentSum, result, currentRootToLeafNodes):
if root is None:
return
currentRootToLeafNodes.append(root.val)
if root.left is None and root.right is None and currentSum + root.val == targetSum:
result.append(list(currentRootToLeafNodes))
else:
self.helper(root.left, targetSum, currentSum + root.val, result, currentRootToLeafNodes)
self.helper(root.right, targetSum, currentSum + root.val, result, currentRootToLeafNodes)
currentRootToLeafNodes.pop()
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<vector<int>> result;
vector<int> currentRootToLeafNodes;
helper(root, targetSum, 0, result, currentRootToLeafNodes);
return result;
}
private:
void helper(TreeNode* root, int targetSum, int currentSum, vector<vector<int>>& result, vector<int>& currentRootToLeafNodes) {
if (root == nullptr) return;
currentRootToLeafNodes.push_back(root->val);
if (root->left == nullptr && root->right == nullptr && currentSum + root->val == targetSum) {
result.push_back(currentRootToLeafNodes);
} else {
helper(root->left, targetSum, currentSum + root->val, result, currentRootToLeafNodes);
helper(root->right, targetSum, currentSum + root->val, result, currentRootToLeafNodes);
}
currentRootToLeafNodes.pop_back();
}
};
Time/Space Complexity:
- Time Complexity: O(n)
- Space Complexity: O(n)
Explanation:
It's a classic backtracking problem, and as always, we declare our result and helper function. With currentRootToLeafNodes we keep the current list of candidates that form a path from root to leaf and we check if we're at leaf node (root.left == null && root.right == null, our base case), and if the currentSum + leaf node value == targetSum, if it is we add that list forming root to leaf path to our result list of lists. However, if we're not at our base case we traverse the left and right subtree. Finally, when we're done with both left and right subtree (or our base case) we backtrack and remove the current node from our current path. Time and space complexity are linear since we're traversing all the nodes in tree and for space complexity, we have the recursion stack which can be at most n (height of skewed tree, all nodes on the left or right side).