Balanced Binary Tree

---

Balanced Binary Tree: Given a binary tree, determine if it is height-balanced. A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Example 1:

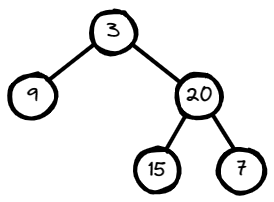
Input: root = [3,9,20,null,null,15,7]
Output: true

---

Example 2:

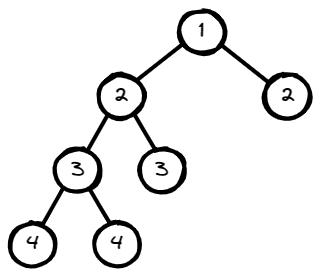
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

---

Example 3:

Input: root = []
Output: true

---

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -10^4 <= Node.val <= 10^4

---

Try this Problem on your own or check similar problems:

1. Maximum Depth of Binary Tree

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
  boolean isBalanced = true;
  public boolean isBalanced(TreeNode root) {
      helper(root);
      return isBalanced;
  }

  private int helper(TreeNode root){
      if(root == null) return 0;
      int left = helper(root.left);
      int right  = helper(root.right);
      if(Math.abs(left - right) > 1) isBalanced = false;
      return Math.max(left, right) + 1;
  }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function (root) {
  let isBalanced = true;
  helper(root);
  return isBalanced;

  function helper(root) {
    if (root === null) return 0;
    let left = helper(root.left);
    let right = helper(root.right);
    if (Math.abs(left - right) > 1) isBalanced = false;
    return Math.max(left, right) + 1;
  }
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    isBalanced = True
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        self.helper(root)
        return self.isBalanced

    def helper(self, root):
        if root is None:
            return 0
        left = self.helper(root.left)
        right = self.helper(root.right)
        if abs(left - right) > 1:
            self.isBalanced = False
        return max(left, right) + 1

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    bool balanced = true;
    int helper(TreeNode* root) {
        if (root == nullptr) return 0;
        int left = helper(root->left);
        int right = helper(root->right);
        if (abs(left - right) > 1) balanced = false;
        return std::max(left, right) + 1;
    }
public:
    bool isBalanced(TreeNode* root) {
        helper(root);
        return balanced;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We traverse all the nodes in the tree leading to linear time complexity O(n) where n is the number of nodes, but we also have linear space complexity since we can have for example a skewed tree (all nodes on left subtree) and then we would keep n recursive calls on the stack. We keep a global isBalanced variable which will be returned as final solution and each time we get height of left and right subtree we check if their (absolute) difference is larger than 1, and if it is we set the isBalanced to false. We then return the height for the current node which is just the maximum height of its left and right subtree incremented by one (counting for the current node). Note that height and depth of a node are different concepts, height of a node is defined as number of nodes between the node and its most distant leaf node, while depth is defined as number of nodes between the node and the root of the tree.