Invert A Binary Tree

---

Invert A Binary Tree: Given the root of a binary tree, invert the tree, and return its root.

Example 1:

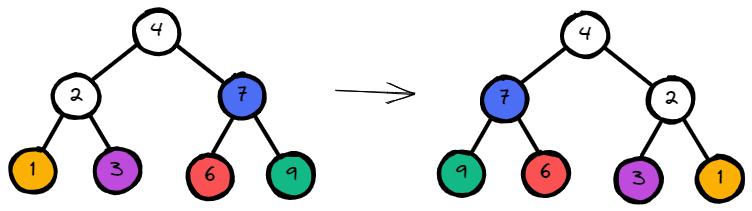
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

---

Example 2:

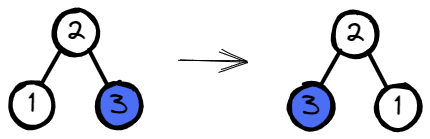
Input: root = [2,1,3]
Output: [2,3,1]

---

Example 2:

Input: root = []
Output: []

---

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• -100 <= Node.val <= 100

---

Try this Problem on your own or check similar problems:

1. Reverse Odd Levels of Binary Tree

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) return null;
        TreeNode temp = root.left;
        root.left = invertTree(root.right);
        root.right = invertTree(temp);
        return root;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function (root) {
  if (root === null) return null;
  let temp = root.left;
  root.left = invertTree(root.right);
  root.right = invertTree(temp);
  return root;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if root is None:
            return None
        temp = root.left
        root.left = self.invertTree(root.right)
        root.right = self.invertTree(temp)
        return root

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return nullptr;
        TreeNode* temp = root->left;
        root->left = invertTree(root->right);
        root->right = invertTree(temp);
        return root;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We use DFS (Depth First Search) approach, to traverse and invert tree, the only trap here is to consider destructive action on left subtree. We use temp value to invert left subtree and assign it as right subtree (same as swapping two int values using a temp helper variable). Since we're traversing the whole binary tree we will have linear time complexity proportional to the number of nodes in binary tree O(n), while for the space complexity if we have left or right skewed tree (every node is left child of its parent, and only node in its level or right child for right skewed tree) we would have a recursion stack of depth n (number of nodes in binary tree) leading to linear space complexity O(n).