Kth Smallest Element in a BST

Kth Smallest Element in a BST: Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

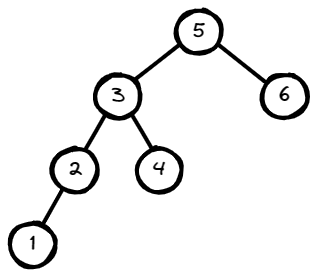
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

The number of nodes in the tree is n.
1 <= k <= n <= 10^4
0 <= Node.val <= 10^4

Try this Problem on your own or check similar problems:

Solution:

Java
JavaScript
Python
C++

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Map<TreeNode, Integer> numberOfLeftChildren = new HashMap<>();
        buildNumberofChildrenMaps(root, numberOfLeftChildren);
        return helper(root, k, numberOfLeftChildren).val;
    }

    private int buildNumberofChildrenMaps(TreeNode root, Map<TreeNode, Integer> numberOfLeftChildren){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;

        int left = buildNumberofChildrenMaps(root.left, numberOfLeftChildren);
        int right = buildNumberofChildrenMaps(root.right, numberOfLeftChildren);

        numberOfLeftChildren.put(root, left);

        return left + right + 1;
    }

    private TreeNode helper(TreeNode root, int k, Map<TreeNode, Integer> numberOfLeftChildren){
        if(k == numberOfLeftChildren.getOrDefault(root, 0) + 1) return root;

        if(k < numberOfLeftChildren.getOrDefault(root, 0) + 1) return helper(root.left, k, numberOfLeftChildren);

        return helper(root.right, k - numberOfLeftChildren.getOrDefault(root, 0) - 1, numberOfLeftChildren);
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function (root, k) {
  return helper(root, k).val;
};

function countNodes(root) {
  if (root === null) return 0;
  return 1 + countNodes(root.left) + countNodes(root.right);
}

function helper(root, k) {
  if (root === null) return null;
  const leftCount = countNodes(root.left);

  if (k === leftCount + 1) return root;

  if (k <= leftCount) return helper(root.left, k);

  return helper(root.right, k - leftCount - 1);
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
      return self.helper(root, k).val

    def count_nodes(self, root):
      if not root:
          return 0
      return 1 + self.count_nodes(root.left) + self.count_nodes(root.right)

    def helper(self, root, k):
      if not root:
          return None
      left_count = self.count_nodes(root.left)

      if k == left_count + 1:
          return root

      if k <= left_count:
          return self.helper(root.left, k)

      return self.helper(root.right, k - left_count - 1)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        unordered_map<TreeNode*, int> numberOfLeftChildren;
        buildNumberofChildrenMaps(root, numberOfLeftChildren);
        return helper(root, k, numberOfLeftChildren)->val;
    }

private:
  int buildNumberofChildrenMaps(TreeNode* root, unordered_map<TreeNode*, int>& numberOfLeftChildren) {
    if (root == nullptr) return 0;
    if (root->left == nullptr && root->right == nullptr) return 1;

    int left = buildNumberofChildrenMaps(root->left, numberOfLeftChildren);
    int right = buildNumberofChildrenMaps(root->right, numberOfLeftChildren);

    numberOfLeftChildren[root] = left;

    return left + right + 1;
  }

  TreeNode* helper(TreeNode* root, int k, unordered_map<TreeNode*, int>& numberOfLeftChildren) {
    if (k == numberOfLeftChildren[root] + 1) return root;

    if (k < numberOfLeftChildren[root] + 1)
      return helper(root->left, k, numberOfLeftChildren);

    return helper(
      root->right,
      k - numberOfLeftChildren[root] - 1,
      numberOfLeftChildren
    );
  }
};

Time/Space Complexity:

Time Complexity: O(n)
Space Complexity: O(n)

Explanation:

It would be trivial to implement a solution which uses inorder traversal and decrements the counter until we reach count == 0 and just return the value at the node when the counter hits 0. We use wrapper class so we can pass the count and value by reference, and we iterate over until there is no left children left, and then go back to the root and traverse the right subtree.

Java
JavaScript
Python
C++

class Solution {
    public class ResultWrapper{
        int count, value;
        ResultWrapper(int count) {
            this.count = count;
        }
    }
    public int kthSmallest(TreeNode root, int k) {
        ResultWrapper result = new ResultWrapper(k);
        helper(root, result);
        return result.value;
    }

    private void helper(TreeNode root, ResultWrapper result){
        if(root.left != null) helper(root.left, result);
        if(--result.count == 0){
            result.value = root.val;
            return;
        }
        if(root.right != null) helper(root.right, result);
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function (root, k) {
  var result = { count: k, value: 0 };
  helper(root, result);
  return result.value;
};

var helper = function (root, result) {
  if (root.left !== null) helper(root.left, result);
  if (--result.count === 0) {
    result.value = root.val;
    return;
  }
  if (root.right !== null) helper(root.right, result);
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    class ResultWrapper:
        def __init__(self, count):
            self.count = count
            self.value = None

    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        result = self.ResultWrapper(k)
        self.helper(root, result)
        return result.value


    def helper(self, root: TreeNode, result: ResultWrapper) -> None:
        if root.left is not None:
            self.helper(root.left, result)
        result.count -= 1
        if result.count == 0:
            result.value = root.val
            return
        if root.right is not None:
            self.helper(root.right, result)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        ResultWrapper result(k);
        helper(root, result);
        return result.value;
    }

private:
   struct ResultWrapper {
        int count;
        int value;
        ResultWrapper(int count) : count(count), value(0) {}
  };
  void helper(TreeNode* root, ResultWrapper& result) {
      if (root->left != nullptr)
          helper(root->left, result);
      --result.count;
      if (result.count == 0) {
          result.value = root->val;
          return;
      }
      if (root->right != nullptr)
          helper(root->right, result);
  }
};

The time and space complexity would be O(n) (space because of recursion stack, and time since we iterate over all nodes). But in the Solution section another approach is suggested which can be utilized if we're allowed to change the structure of BST class for future queries, for each node we would track the number of left children (in the solution we're doing this with helper data structure a map that tracks the number of left children for each of the nodes, we build the map using buildNumberofChildrenMaps). Then how do we use that information to find the kth smallest element? We traverse the tree and for each node we check if the number of left children is k-1 (in our code k == numberOfLeftChildren.getOrDefault(root, 0) + 1) and if it is we just return the value of the current node since it is the kth smallest element, otherwise we have two scenario. Current node is far from the kth smallest so we go deeper into the left subtree or current node is smaller than the kth smallest so we have to the right subtree (this time searching for k - x element, where x is the index of current node in sorted order).

Example 1:​

Example 2:​

Constraints:​

Solution:​

Time/Space Complexity:​