Path Sum

---

Path Sum: Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

A leaf is a node with no children.

Example 1:

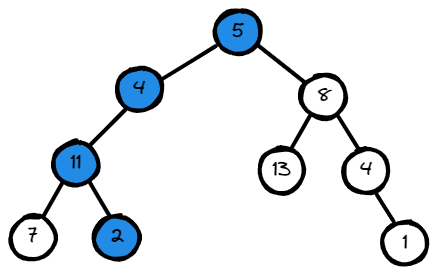
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.

---

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false
Explanation: There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.

---

Example 3:

Input: root = [], targetSum = 0
Output: false
Explanation: Since the tree is empty, there are no root-to-leaf paths.

---

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

---

Try this Problem on your own or check similar problems:

1. Path Sum II
2. Sum Root to Leaf Numbers
3. Path Sum III

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        return helper(root, 0, targetSum);
    }

    private boolean helper(TreeNode root, int currSum, int targetSum){
        if(root == null) return false;

        if(root.left == null && root.right == null) return currSum + root.val == targetSum;

        return helper(root.left, currSum + root.val, targetSum) ||
                    helper(root.right, currSum + root.val, targetSum);
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function (root, targetSum) {
  return helper(root, 0, targetSum);
};

function helper(root, currSum, targetSum) {
  if (root === null) return false;

  if (root.left === null && root.right === null)
    return currSum + root.val === targetSum;

  return (
    helper(root.left, currSum + root.val, targetSum) ||
    helper(root.right, currSum + root.val, targetSum)
  );
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        return self.helper(root, 0, targetSum)

    def helper(self, root, currSum, targetSum):
        if root is None:
            return False

        if root.left is None and root.right is None:
            return currSum + root.val == targetSum

        return (
            self.helper(root.left, currSum + root.val, targetSum) or
            self.helper(root.right, currSum + root.val, targetSum)
        )

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        return helper(root, 0, targetSum);
    }

private:
    bool helper(TreeNode* root, int currSum, int targetSum) {
        if (root == nullptr) return false;

        if (root->left == nullptr && root->right == nullptr)
            return currSum + root->val == targetSum;

        return (
            helper(root->left, currSum + root->val, targetSum) ||
            helper(root->right, currSum + root->val, targetSum)
        );
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We use the DFS (depth first search) just like in Same Tree and keep the currentSum variable to track the path sum, up to leaf node (note that we could have gone without it, subtract values from targetSum and check if at leaves we have 0 for targetSum). We have base case where node is leaf and then we check if currSum + root.val == targetSum, otherwise we go deeper into the tree by checking both left and right subtree in DFS fashion. We will cover all nodes, so the time complexity is O(n), and space complexity in worst case is O(n) if the tree is left or right skewed.