Lowest Common Ancestor of a Binary Search Tree

---

Lowest Common Ancestor of a Binary Search Tree: Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).

Example 1:

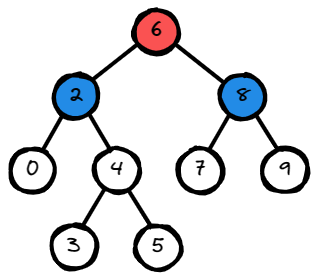
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

---

Example 2:

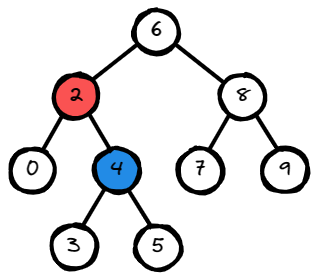
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since
a node can be a descendant of itself according to the LCA definition.

---

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

---

Constraints:

• The number of nodes in the tree is in the range [2, 10^5].
• -10^9 <= Node.val <= 10^9
• All Node.val are unique.
• p != q
• p and q will exist in the BST.

---

Try this Problem on your own or check similar problems:

1. Lowest Common Ancestor of a Binary Tree
2. Lowest Common Ancestor of a Binary Tree II

Solution:

Java

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
    else if(root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
    return root;
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  if (root.val > p.val && root.val > q.val) {
    return lowestCommonAncestor(root.left, p, q);
  } else if (root.val < p.val && root.val < q.val) {
    return lowestCommonAncestor(root.right, p, q);
  } else {
    return root;
  }
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if root.val > p.val and root.val > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        elif root.val < p.val and root.val < q.val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return root

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root->val > p->val && root->val > q->val)
            return lowestCommonAncestor(root->left, p, q);
        else if (root->val < p->val && root->val < q->val)
            return lowestCommonAncestor(root->right, p, q);
        else
            return root;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(h) where h is the height of tree
• Space Complexity: O(h)

---

Explanation:

We have a binary search tree where for each node n we have all nodes with smaller values in the left subtree, while all the nodes with larger values in the right subtree. To search in a BST, we spend at most log n = h = height of tree time and space (for recursion). We can utilize the property of BST to find the lowest common ancestor as we have three scenarios:

• The root.val is larger than both p and q so we can decrease it and go left (find nodes with smaller value)
• The root.val is smaller than both p and q so we can increase it and go right (find nodes with larger value)
• The root.val is larger (or equal) than the value of one of the nodes p and q and smaller (or equal) than value of the other, so we have found the common ancestor

Let's also transform the recursive version to the iterative one (saving on space complexity):

Java

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
   while (root != null) {
      if (root.val > p.val && root.val > q.val) {
          root = root.left;
      } else if (root.val < p.val && root.val < q.val) {
          root = root.right;
      } else {
          return root;
      }
    }
    return null;
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  while (root) {
    if (root.val > p.val && root.val > q.val) {
      root = root.left;
    } else if (root.val < p.val && root.val < q.val) {
      root = root.right;
    } else {
      return root;
    }
  }
  return null;
};

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
       while (root) {
          if (root.val > p.val && root.val > q.val) {
              root = root.left;
          } else if (root.val < p.val && root.val < q.val) {
              root = root.right;
          } else {
              return root;
          }
      }
      return null;

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while (root) {
            if (root.val > p.val && root.val > q.val) {
                root = root.left;
            } else if (root.val < p.val && root.val < q.val) {
                root = root.right;
            } else {
                return root;
            }
        }
        return null;
    }
};