Convert Sorted Array to Binary Search Tree

---

Convert Sorted Array to Binary Search Tree: Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree. A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Example 1:

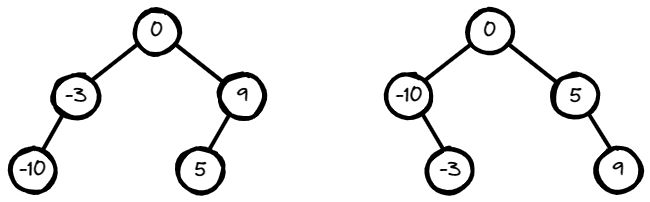
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted.

---

Example 2:

Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

---

Constraints:

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums is sorted in a strictly increasing order.

---

Try this Problem on your own or check similar problems:

1. Convert Sorted List to Binary Search Tree

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums, 0, nums.length - 1);
    }

    private TreeNode helper(int[] nums, int start, int end){
      if(start > end) return null;
      int mid = start + (end - start) / 2;
      TreeNode root = new TreeNode(nums[mid]);
      root.left = helper(nums, start, mid - 1);
      root.right = helper(nums, mid + 1, end);
      return root;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var sortedArrayToBST = function (nums) {
  return helper(nums, 0, nums.length - 1);
};

function helper(nums, start, end) {
  if (start > end) return null;
  const mid = Math.floor((start + end) / 2);
  const root = new TreeNode(nums[mid]);
  root.left = helper(nums, start, mid - 1);
  root.right = helper(nums, mid + 1, end);
  return root;
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        return self.helper(nums, 0, len(nums) - 1)

    def helper(self, nums, start, end):
        if start > end:
            return None
        mid = (start + end) // 2
        root = TreeNode(nums[mid])
        root.left = self.helper(nums, start, mid - 1)
        root.right = self.helper(nums, mid + 1, end)
        return root

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

private:
    TreeNode* helper(vector<int>& nums, int start, int end) {
        if (start > end) return nullptr;
        int mid = start + (end - start) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, start, mid - 1);
        root->right = helper(nums, mid + 1, end);
        return root;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(logn)

---

Explanation:

The algorithm for getting balanced binary search tree (BST) is simple when we have a sorted array as input since we can just pick the middle index array element as value for the root and recursively build the left and right subtree using the left and right side of middle element in the input array respectively. Note that we calculate middle element start + (end - start) / 2 it produces the same result as (start + end) / 2 but it copes with overflow if the boundaries are large integers. Total time complexity is proportional to the input array elements, while since we have height balanced tree total space complexity spend on recursion stack will be the height of the tree O(logn). We return the new formed root as our final solution.