Same Tree

---

Same Tree: Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

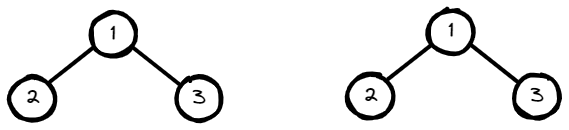
Input: p = [1,2,3], q = [1,2,3]
Output: true

---

Example 2:

Input: p = [1,2], q = [1,null,2]
Output: false

---

Example 3:

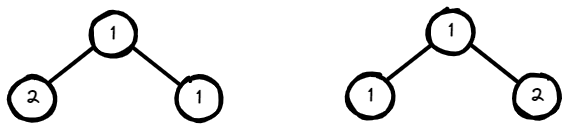
Input: p = [1,2,1], q = [1,1,2]
Output: false

---

Constraints:

• The number of nodes in both trees is in the range [0, 100].
• -10^4 <= Node.val <= 10^4

---

Try this Problem on your own or check similar problems:

1. Search in a Binary Search Tree
2. Lowest Common Ancestor of Deepest Leaves
3. Find Elements in a Contaminated Binary Tree

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        return helper(p, q);
    }

    private boolean helper(TreeNode p, TreeNode q){
        if(p == null || q == null) return p == q;
        return p.val == q.val && helper(p.left, q.left) && helper(p.right, q.right);
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
  return helper(p, q);
};

function helper(p, q) {
  if (p === null || q === null) return p === q;
  return p.val === q.val && helper(p.left, q.left) && helper(p.right, q.right);
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        return self.helper(p, q)

    def helper(self, p, q):
        if p is None or q is None:
            return p == q
        return p.val == q.val and self.helper(p.left, q.left) and self.helper(p.right, q.right)

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        return helper(p, q);
    }

private:
    bool helper(TreeNode* p, TreeNode* q) {
        if (p == nullptr || q == nullptr)
            return p == q;
        return p->val == q->val && helper(p->left, q->left) && helper(p->right, q->right);
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We use the DFS (depth first search) to check if each node in p corresponds to each node in q. If a node in one tree is null we check if the corresponding node in the other tree is also null and return false if not. Think of it as two trees are the same if the value of both roots is same and if their left and right subtrees are the same (leading to recursive approach). Worst case scenario for space complexity is the recursion stack size if all the nodes are on one side (left or right subtree) because in that case we would call the function n times (O(n) space complexity). Time is linear to the number of nodes in the smaller tree (early termination once we hit the leaf node of smaller tree with n nodes).