Merge Two Binary Trees

---

Merge Two Binary Trees: You are given two binary trees root1 and root2.

Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

Return the merged tree.

Note: The merging process must start from the root nodes of both trees.

Example 1:

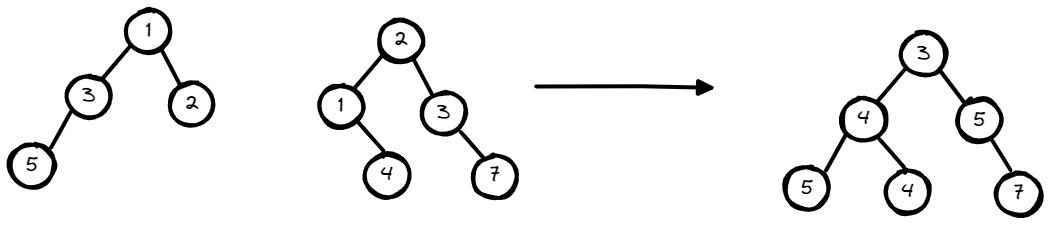
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]

---

Example 2:

Input: root = [1,2]
Output: 1

---

Constraints:

• The number of nodes in both trees is in the range [0, 2000].
• -10^4 <= Node.val <= 10^4

---

Try this Problem on your own or check similar problems:

1. Redundant Connection
2. Shortest Path in Hidden Grid
3. Nearest Exit from Entrance in Maze

Solution:

Java

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        TreeNode root = new TreeNode();
        return helper(root1, root2, root);
    }
    private TreeNode helper(TreeNode root1, TreeNode root2, TreeNode root){
        if(root1 == null || root2 == null) return root1 == null ? root2 : root1;
        root.val = root1.val + root2.val;
        root.left = helper(root1.left, root2.left, new TreeNode());
        root.right = helper(root1.right, root2.right, new TreeNode());
        return root;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function (root1, root2) {
  let root = new TreeNode();
  return helper(root1, root2, root);
};

function helper(root1, root2, root) {
  if (root1 === null || root2 === null) return root1 === null ? root2 : root1;
  root.val = root1.val + root2.val;
  root.left = helper(root1.left, root2.left, new TreeNode());
  root.right = helper(root1.right, root2.right, new TreeNode());
  return root;
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        root = TreeNode()
        return self.helper(root1, root2, root)

    def helper(self, root1, root2, root):
        if root1 is None or root2 is None:
            return root2 if root1 is None else root1
        root.val = root1.val + root2.val
        root.left = self.helper(root1.left, root2.left, TreeNode())
        root.right = self.helper(root1.right, root2.right, TreeNode())
        return root

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        TreeNode* root = new TreeNode(0);
        return helper(root1, root2, root);
    }

private:
    TreeNode* helper(TreeNode* root1, TreeNode* root2, TreeNode* root) {
        if (root1 == nullptr || root2 == nullptr)
            return root1 == nullptr ? root2 : root1;
        root->val = root1->val + root2->val;
        root->left = helper(root1->left, root2->left, new TreeNode(0));
        root->right = helper(root1->right, root2->right, new TreeNode(0));
        return root;
    }
};

---

Time/Space Complexity:

• Time Complexity: O(m)
• Space Complexity: O(m)

---

Explanation:

First notice that we short-circuit the helper calls if one of the trees subtrees (or the whole tree) is null leading to time and space complexity to O(m) where m is the number of nodes of the smaller tree (since we're not counting the allocated space for resulting tree). First, we calculate the aggregate (sum) value if both trees are not null, and then we recursively build up the left and right subtree in DFS manner and return the new root. You can make a point that we can reuse one of the trees and transform to result without allocating more memory but be aware that destructive operation on the old tree will cause the nodes in the new tree to be gone too.