Serialize and Deserialize Binary Tree

---

Serialize and Deserialize Binary Tree: Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Example 1:

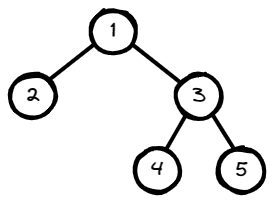
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

---

Example 2:

Input: root = []
Output: []

---

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 10^4].
• -1000 <= Node.val <= 1000

---

Try this Problem on your own or check similar problems:

1. Serialize and Deserialize BST
2. Find Duplicate Subtrees

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
      if(root == null) return "";
      StringBuilder sb = new StringBuilder();
      buildSerialization(root, sb);
      return sb.toString();
    }

    private void buildSerialization(TreeNode root, StringBuilder sb){
      if(root == null){
          sb.append("X").append(",");
          return;
      }
      sb.append(root.val).append(",");
      buildSerialization(root.left, sb);
      buildSerialization(root.right, sb);
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
      if(data == "") return null;
      Queue<String> q = new LinkedList<>(Arrays.asList(data.split(",")));
      return buildTree(q);
    }

    private TreeNode buildTree(Queue<String> q){
      String val = q.poll();
      if(val.equals("X")) return null;
      TreeNode root = new TreeNode(Integer.valueOf(val));
      root.left = buildTree(q);
      root.right = buildTree(q);
      return root;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * Encodes a tree to a single string.
 *
 * @param {TreeNode} root
 * @return {string}
 */
var serialize = function (root) {
  if (root === null) return "";
  var sb = [];
  buildSerialization(root, sb);
  return sb.join(",");
};

function buildSerialization(root, sb) {
  if (root === null) {
    sb.push("X");
    return;
  }
  sb.push(root.val.toString());
  buildSerialization(root.left, sb);
  buildSerialization(root.right, sb);
}

/**
 * Decodes your encoded data to tree.
 *
 * @param {string} data
 * @return {TreeNode}
 */
var deserialize = function (data) {
  if (data === "") return null;
  var values = data.split(",");
  var queue = values.slice();
  return buildTree(queue);
};

function buildTree(queue) {
  var val = queue.shift();
  if (val === "X") return null;
  var root = new TreeNode(parseInt(val));
  root.left = buildTree(queue);
  root.right = buildTree(queue);
  return root;
}

/**
 * Your functions will be called as such:
 * deserialize(serialize(root));
 */

Python

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.

        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return ""
        serialized = []
        self.buildSerialization(root, serialized)
        return ",".join(serialized)

    def buildSerialization(self, root, serialized):
        if not root:
            serialized.append("X")
            return
        serialized.append(str(root.val))
        self.buildSerialization(root.left, serialized)
        self.buildSerialization(root.right, serialized)


    def deserialize(self, data):
        """Decodes your encoded data to tree.

        :type data: str
        :rtype: TreeNode
        """
        if not data:
            return None
        values = data.split(",")
        queue = values.copy()
        return self.buildTree(queue)

    def buildTree(self, queue):
        val = queue.pop(0)
        if val == "X":
            return None
        root = TreeNode(int(val))
        root.left = self.buildTree(queue)
        root.right = self.buildTree(queue)
        return root


# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
         if (!root)
            return "";
        vector<string> serialized;
        buildSerialization(root, serialized);
        stringstream ss;
        for (const string& s : serialized)
            ss << s << ",";
        return ss.str();
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
         if (data.empty())
            return NULL;
        vector<string> values;
        stringstream ss(data);
        string token;
        while (getline(ss, token, ','))
            values.push_back(token);
        queue<string> q;
        for (const string& val : values)
            q.push(val);
        return buildTree(q);
    }

private:
    void buildSerialization(TreeNode* root, vector<string>& serialized) {
      if (!root) {
          serialized.push_back("X");
          return;
      }
      serialized.push_back(to_string(root->val));
      buildSerialization(root->left, serialized);
      buildSerialization(root->right, serialized);
    }

    TreeNode* buildTree(queue<string>& q) {
        string val = q.front();
        q.pop();
        if (val == "X")
            return NULL;
        TreeNode* root = new TreeNode(stoi(val));
        root->left = buildTree(q);
        root->right = buildTree(q);
        return root;
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

---

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(n)

---

Explanation:

We use StringBuilder and Queue for serialize and deserialize which leads us to linear space complexity, we traverse all nodes in the tree (and all characters in serialization) leading to linear time complexity too. In the Construct Binary Tree from Preorder and Inorder Traversal we needed both inorder and preorder traversals to build the tree. Note that we needed preorder to determine what is the root of the current subtree, and we needed inorder to determine the left and right subtree size for each node. But in this problem, we're not bounded by already defined formats of traversals. So we could utilize the preorder but this time also marking the end of each node's left and right subtree with 'X' which leads to 1,2,X,X,3,4,X,X,5,X,X, preorder sequence for the given example, so for serialize we do a preorder on the tree and build the string with X as markers for end of substrees. For deserialize we use a queue so we can keep track of the current val in the serialization, and each time we hit 'X' we know the subtree ends there and we return null. We recursively build the left and right subtree.