Construct Binary Tree from Preorder and Inorder Traversal
Construct Binary Tree from Preorder and Inorder Traversal:
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Example 1:
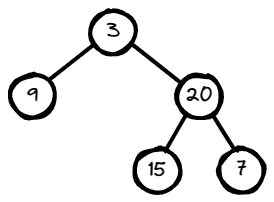
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
Example 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
Constraints:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorderandinorderconsist of unique values.- Each value of
inorderalso appears inpreorder. preorderis guaranteed to be the preorder traversal of the tree.inorderis guaranteed to be the inorder traversal of the tree.
Try this Problem on your own or check similar problems:
Solution:
- Java
- JavaScript
- Python
- C++
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
Map<Integer, Integer> inorderIdx = new HashMap<>();
for(int i = 0; i < inorder.length; ++i){
inorderIdx.put(inorder[i], i);
}
return constructTree(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1, inorderIdx);
}
private TreeNode constructTree(int[] preorder, int[] inorder, int preorderStart, int preorderEnd, int inorderStart, int inorderEnd, Map<Integer,Integer> inorderIdx){
if(preorderStart > preorderEnd || inorderStart > inorderEnd) return null;
TreeNode root = new TreeNode(preorder[preorderStart]);
int idx = inorderIdx.get(preorder[preorderStart]);
int leftSizeLength = idx - inorderStart;
root.left = constructTree(preorder, inorder, preorderStart + 1, preorderStart + leftSizeLength, inorderStart, idx - 1, inorderIdx);
root.right = constructTree(preorder, inorder, preorderStart + leftSizeLength + 1, preorderEnd, idx + 1, inorderEnd, inorderIdx);
return root;
}
}
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} preorder
* @param {number[]} inorder
* @return {TreeNode}
*/
var buildTree = function (preorder, inorder) {
const inorderIdx = new Map();
for (let i = 0; i < inorder.length; ++i) {
inorderIdx.set(inorder[i], i);
}
return constructTree(
preorder,
inorder,
0,
preorder.length - 1,
0,
inorder.length - 1,
inorderIdx
);
};
function constructTree(
preorder,
inorder,
preorderStart,
preorderEnd,
inorderStart,
inorderEnd,
inorderIdx
) {
if (preorderStart > preorderEnd || inorderStart > inorderEnd) return null;
const root = new TreeNode(preorder[preorderStart]);
const idx = inorderIdx.get(preorder[preorderStart]);
const leftSizeLength = idx - inorderStart;
root.left = constructTree(
preorder,
inorder,
preorderStart + 1,
preorderStart + leftSizeLength,
inorderStart,
idx - 1,
inorderIdx
);
root.right = constructTree(
preorder,
inorder,
preorderStart + leftSizeLength + 1,
preorderEnd,
idx + 1,
inorderEnd,
inorderIdx
);
return root;
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
inorderIdx = {val: idx for idx, val in enumerate(inorder)}
return self.constructTree(preorder, inorder, 0, len(preorder) - 1, 0, len(inorder) - 1, inorderIdx)
def constructTree(self, preorder, inorder, preorderStart, preorderEnd, inorderStart, inorderEnd, inorderIdx):
if preorderStart > preorderEnd or inorderStart > inorderEnd:
return None
root = TreeNode(preorder[preorderStart])
idx = inorderIdx[preorder[preorderStart]]
leftSizeLength = idx - inorderStart
root.left = self.constructTree(preorder, inorder, preorderStart + 1, preorderStart + leftSizeLength, inorderStart, idx - 1, inorderIdx)
root.right = self.constructTree(preorder, inorder, preorderStart + leftSizeLength + 1, preorderEnd, idx + 1, inorderEnd, inorderIdx)
return root
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
unordered_map<int, int> inorderIdx;
for (int i = 0; i < inorder.size(); ++i) {
inorderIdx[inorder[i]] = i;
}
return constructTree(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1, inorderIdx);
}
private:
TreeNode* constructTree(vector<int>& preorder, vector<int>& inorder, int preorderStart, int preorderEnd, int inorderStart, int inorderEnd, unordered_map<int, int>& inorderIdx) {
if (preorderStart > preorderEnd || inorderStart > inorderEnd) return nullptr;
TreeNode* root = new TreeNode(preorder[preorderStart]);
int idx = inorderIdx[preorder[preorderStart]];
int leftSizeLength = idx - inorderStart;
root->left = constructTree(preorder, inorder, preorderStart + 1, preorderStart + leftSizeLength, inorderStart, idx - 1, inorderIdx);
root->right = constructTree(preorder, inorder, preorderStart + leftSizeLength + 1, preorderEnd, idx + 1, inorderEnd, inorderIdx);
return root;
}
};
Time/Space Complexity:
- Time Complexity: O(n)
- Space Complexity: O(n)
Explanation:
It's important to remember what preorder and inorder are:
- Preorder visits root first, then the left subtree than the right subtree
- Inorder visits left subtree first, then the root, and finally right subtree.
So, we can use the preorder to determine our root, since the first element of the array will represent the root. Why do we need the inorder? Well, we need to know how big the left and right subtrees are, if we find the root value in the inorder input array, we know that on its left we have value of nodes appearing in the left subtree while on the right side of it we have value of nodes appearing in its right subtree. Since we don't want to traverse the inorder input array everytime we search for a root we need a faster lookup that's why we defined inorderIdx which just maps the element in inorder input array to its index. We recursively construct the tree by:
- First picking the root as the start of the
preorderarray, and its index in theinorderso we can calculate the size of its left subtree (knowing the size of the left, we implicitly know the size of the right subtree). - We build the left subtree by starting with the next element in
preorderarray and usingleftSizeLengthto determine how far we go for left subtree, note that we only need elements beforeidxin theinorderarray. - We build the right subtree starting just after the elements of left subtree
preorderStart + leftSizeLength + 1(and going to end), note that we only need elements afteridxin theinorderarray for the right subtree.
The time and space complexity are linear to the size of input arrays, since we traverse through each of the elements and for space, we have recursion stack and the inorderIdx map.