Flood Fill

---

Flood Fill: An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.

You are also given three integers sr, sc, and color. You should perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with color.

Return the modified image after performing the flood fill.

Example 1:

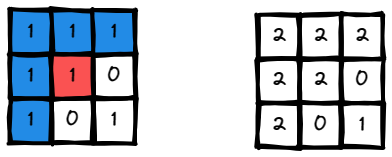
Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation: From the center of the image with position
(sr, sc) = (1, 1) (i.e., the red pixel),
all pixels connected by a path of the same color as the starting pixel
(i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not 4-directionally
connected to the starting pixel.

---

Example 2:

Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
Output: [[0,0,0],[0,0,0]]
Explanation: The starting pixel is already colored 0,
so no changes are made to the image.

---

Constraints:

• m == image.length
• n == image[i].length
• 1 <= m, n <= 50
• 0 <= image[i][j], color < 2^16
• 0 <= sr < m
• 0 <= sc < n

---

Try this Problem on your own or check similar problems:

1. Island Perimeter

Solution:

Java

class Solution {
    public int[][] floodFill(int[][] image, int sr, int sc, int color) {
        int currentColor = image[sr][sc];
        helper(image, sr, sc, currentColor, color);
        return image;
    }

    private void helper(int[][] image, int row, int column, int currentColor, int color){
        if(row < 0 || row >= image.length || column < 0 || column >= image[0].length || image[row][column] != currentColor) return;
        if(image[row][column] == color) return;

        image[row][column] = color;
        helper(image, row - 1, column, currentColor, color);
        helper(image, row + 1, column, currentColor, color);
        helper(image, row, column - 1, currentColor, color);
        helper(image, row, column + 1, currentColor, color);
    }
}

JavaScript

/**
 * @param {number[][]} image
 * @param {number} sr
 * @param {number} sc
 * @param {number} color
 * @return {number[][]}
 */
var floodFill = function (image, sr, sc, color) {
  const currentColor = image[sr][sc];
  helper(image, sr, sc, currentColor, color);
  return image;
};

function helper(image, row, column, currentColor, color) {
  if (
    row < 0 ||
    row >= image.length ||
    column < 0 ||
    column >= image[0].length ||
    image[row][column] !== currentColor
  )
    return;
  if (image[row][column] === color) return;

  image[row][column] = color;
  helper(image, row - 1, column, currentColor, color);
  helper(image, row + 1, column, currentColor, color);
  helper(image, row, column - 1, currentColor, color);
  helper(image, row, column + 1, currentColor, color);
}

Python

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, color: int) -> List[List[int]]:
        currentColor = image[sr][sc]
        self.helper(image, sr, sc, currentColor, color)
        return image

    def helper(self, image, row, column, currentColor, color):
        if row < 0 or row >= len(image) or column < 0 or column >= len(image[0]) or image[row][column] != currentColor:
            return
        if image[row][column] == color:
            return

        image[row][column] = color
        self.helper(image, row - 1, column, currentColor, color)
        self.helper(image, row + 1, column, currentColor, color)
        self.helper(image, row, column - 1, currentColor, color)
        self.helper(image, row, column + 1, currentColor, color)

C++

class Solution {
public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        int currentColor = image[sr][sc];
        helper(image, sr, sc, currentColor, color);
        return image;
    }

private:
    void helper(std::vector<std::vector<int>>& image, int row, int column, int currentColor, int color) {
        if (row < 0 || row >= image.size() || column < 0 || column >= image[0].size() || image[row][column] != currentColor)
            return;
        if (image[row][column] == color)
            return;

        image[row][column] = color;
        helper(image, row - 1, column, currentColor, color);
        helper(image, row + 1, column, currentColor, color);
        helper(image, row, column - 1, currentColor, color);
        helper(image, row, column + 1, currentColor, color);
    }
};

---

Time/Space Complexity:

• Time Complexity: O(mn)
• Space Complexity: O(mn)

---

Explanation:

We perform Depth-First Search (DFS) on the input matrix by going to all four neighbors in four directions (but doing it depth wise since we will be exhausting one direction until it's out of boundary). It's a standard template on how to do a DFS on matrix like structure:

• You define a helper method taking as parameters the input matrix, current position (row and column) and its current property currentColor and info about the desired property.
• You call the helper method and first check if we're out of boundary with our current position (index or either row or column negative or larger than equal to the size of array), then we check if the color at the position is currentColor and we return from the helper function if it's not.
• We also check if the current position pixel has already been painted to the desired color, so that we don't end in an infinitive loop visiting one pixel again and again, it's the same as if you would keep a matrix visited checking if you already visited every element in the matrix.
• We make the current position pixel our desired color.
• We move down, up, left and right by either incrementing or decrementing row or column.

The time and space complexity are O(mn) which is the size of the matrix since we can traverse all elements and we have recursions stack (space complexity) corresponding to the size of the matrix/grid.